特征
特征是对象的某个变量,在一段时间里面数据所呈现出来的某种特点。
为什么我们要来研究特征,这是因为在工业设备运行和工业生产过程中,任何的 “异常” 或 “问题”,其实都伴随着数据的某种或某些特征的出现。所以,对特征的抓取和研判,是一件非常重要的事情。
我们先直观看一下数据:
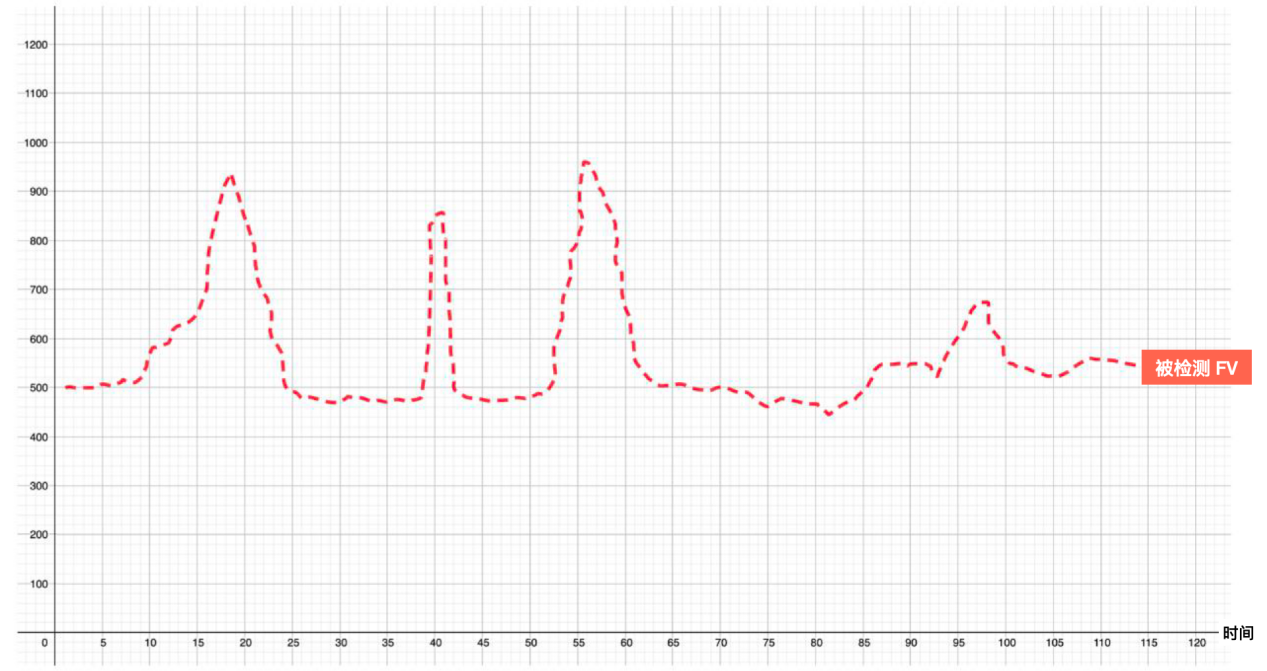
从这个数据曲线很容易发现,被检测FV在 “1分钟内有3次跳跃”:
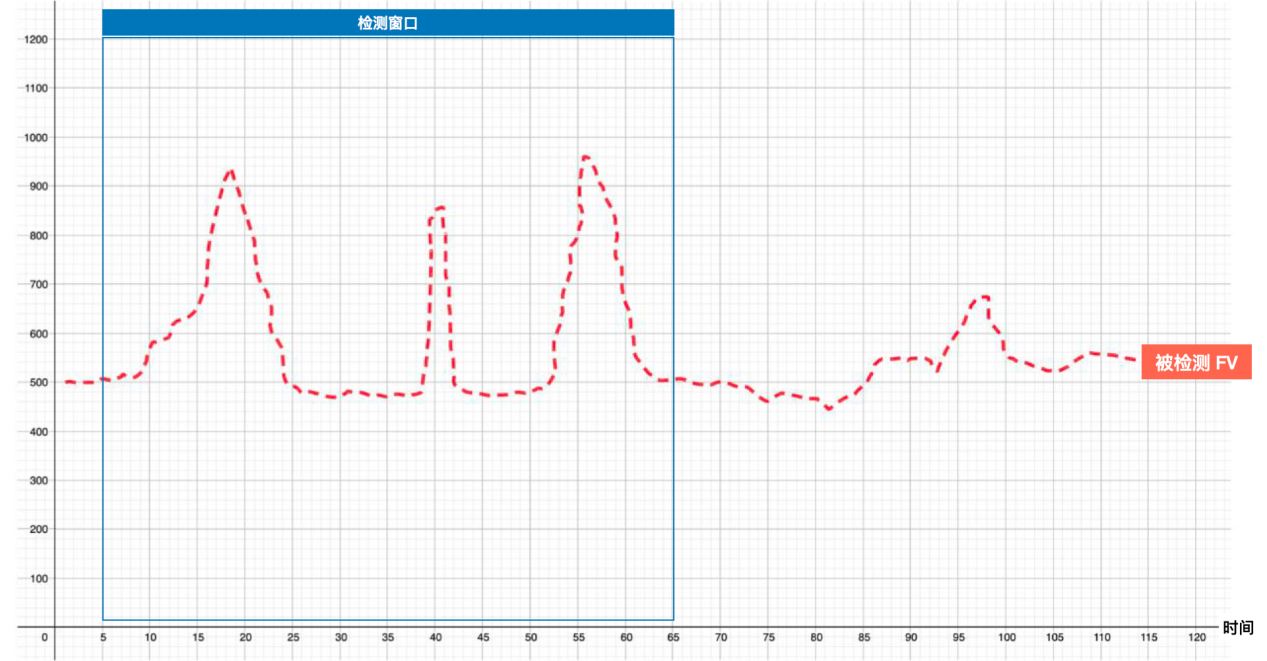
这个就是特征。需要注意的是,这里有几个重要的说法:
一个是 “1分钟内”,就是特征在发生的时间窗口,这叫 “检测窗口”;
另一个是 “跳跃”,这个就是特征;当然,怎么判断 “跳跃”(即跳跃多高才算做是“跳跃”)需要说清楚,也就是说,无论什么特征,一定都是有定量的限定。
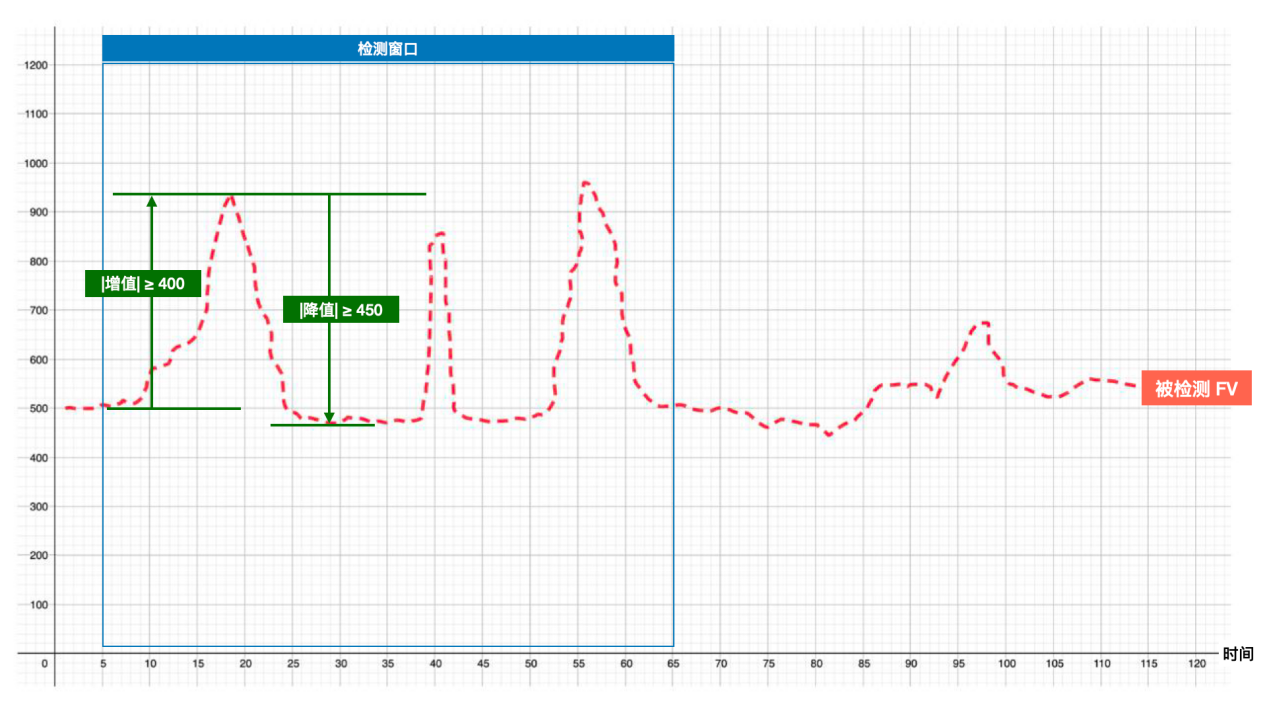
再一个,就是 “3次”。这个实际上等价于把检测窗口分拆成3个,只要在每检测窗口里面出现过1次我们跟踪检测的特征,这个特征就算成立。
关联条件
实际上,特征检测并不像看上去这么简单和直接,它是一个非常复杂的数据分析。这是因为我们经常需要抓取检测的特征,有可能是多因素的,而且还有可能在关注特征本身以外,还需要关注与特征有关的东西,这就是 “关联条件”。
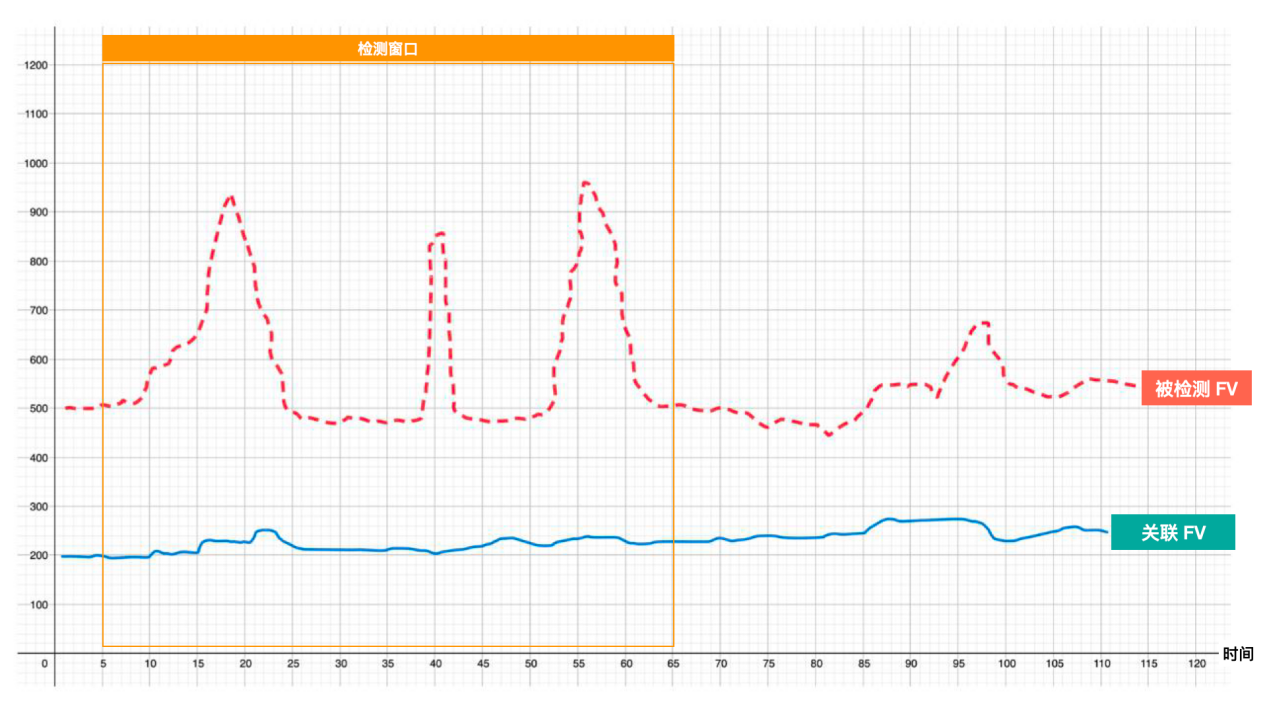
所谓关联条件,是伴随特征出现的时候,其他因素必须同步出现的特征。通常称为 “伴生条件” 或 “关联条件”。
比如,上面这个被检测FV数据在检测窗口中出现了我们关注的跳跃,但这是不是我们正在寻找的特征,还取决于另一个相关FV的情况,是不是基本平稳而没有什么大波动。只有这两个条件(被检测FV出现跳跃,以及关联FV基本平稳)同时成立,才算是特征成立。
被检测FV,称为 “主因素”,而关联FV则称为 “关联因素”。
对关联因素(FV)而言,实际上也是在对其特征进行检测,因为 “平稳” 也是一种特征。但为什么要把这种并行的特征检测分为 “特征” 和 “关联” 呢?这是因为通常会有两个事情同时在进行:一个不包含关联因素,一个包含关联因素。
这是对数据深层次分析的一个基本方法。比如以上面的数据为例,我们往往需要两个结论,一个是主因素有没有出现跳跃特征,还有一个是主因素出现特征的时候,关联因素有没有出现相关特征。
工业数据的实时检测和分析,是工业互联网一个非常重要的作用。MixIOT 体系也是一个非常强大的数据分析系统,除了实时特征检测外,还有其他各种数据分析应用,如各种指数及估计值分析计算等等。这些东西如果用好了,可以起到非常大的作用。
实际工况的特征
前面我们对特征做了一些简单的介绍。特征检测应用,最重要的是要在实际工况中发挥作用,这就需要我们对实际工况的掌握。
我们按特征类型来介绍,这了特征可以应用在什么工况场合,如何使用特征,以及特征检测能起到什么作用。
跳跃特征
跳跃特征是最常见的特征,也是应用最多的特征,比如,JMP(无限定跳跃)就是跳跃特征。
一般来说,跳跃特征使用的典型的工况场合是,去观察哪些本应该连续且缓慢变化的参数变量,有没有出现什么突变或异常。
数据跳跃特征实际上是我们采集到的数据集中的突变点或异常点,之所以说它们是突变点或异常点,是因为这些点与周围的数据点相比有显著的差异。
首先,我们要了解,数据跳跃可能是由多种原因造成的,例如:
- 测量误差:我们的数据实际上都来自传感器的测量,如果测量的过程中出现误差,也可能导致某些数据点与其他数据点显著不同。
- 确为异常值:某些数据点本身可能就是异常值,它们可能是由于某些特定事件或情况造成的,与数据集中的其他数据点不具有相同的分布特性。
- 数据采集错误:数据终端对接控制器,在采集数据的过程中出现错误,也可能导致数据跳跃。
- 自然变异性:在某些情况下,数据跳跃可能是数据集自然变异性的一部分,特别是当数据集包含来自不同群体或条件的数据时。
Mixiot 的强大作用,就是数据处理。因此,我们在处理数据时,识别和理解数据跳跃的原因是很重要的,因为它们可能影响分析结果的准确性。
在某些情况下,可能需要对这些异常点进行进一步的调查或处理,比如,我们在统计的时候,需要建立过滤模型,对数据清洗,以保证统计计算结果不受它们的影响,保证统计计算的准确程度。
跳跃特征是在短时间里面发生的,所以,我们通常不能仅以一个特征的发生,就对实际工况做出判断,而是需要多次观察。
增加检测窗口
比如,我们的数据里面只有冷不丁来一个跳跃:
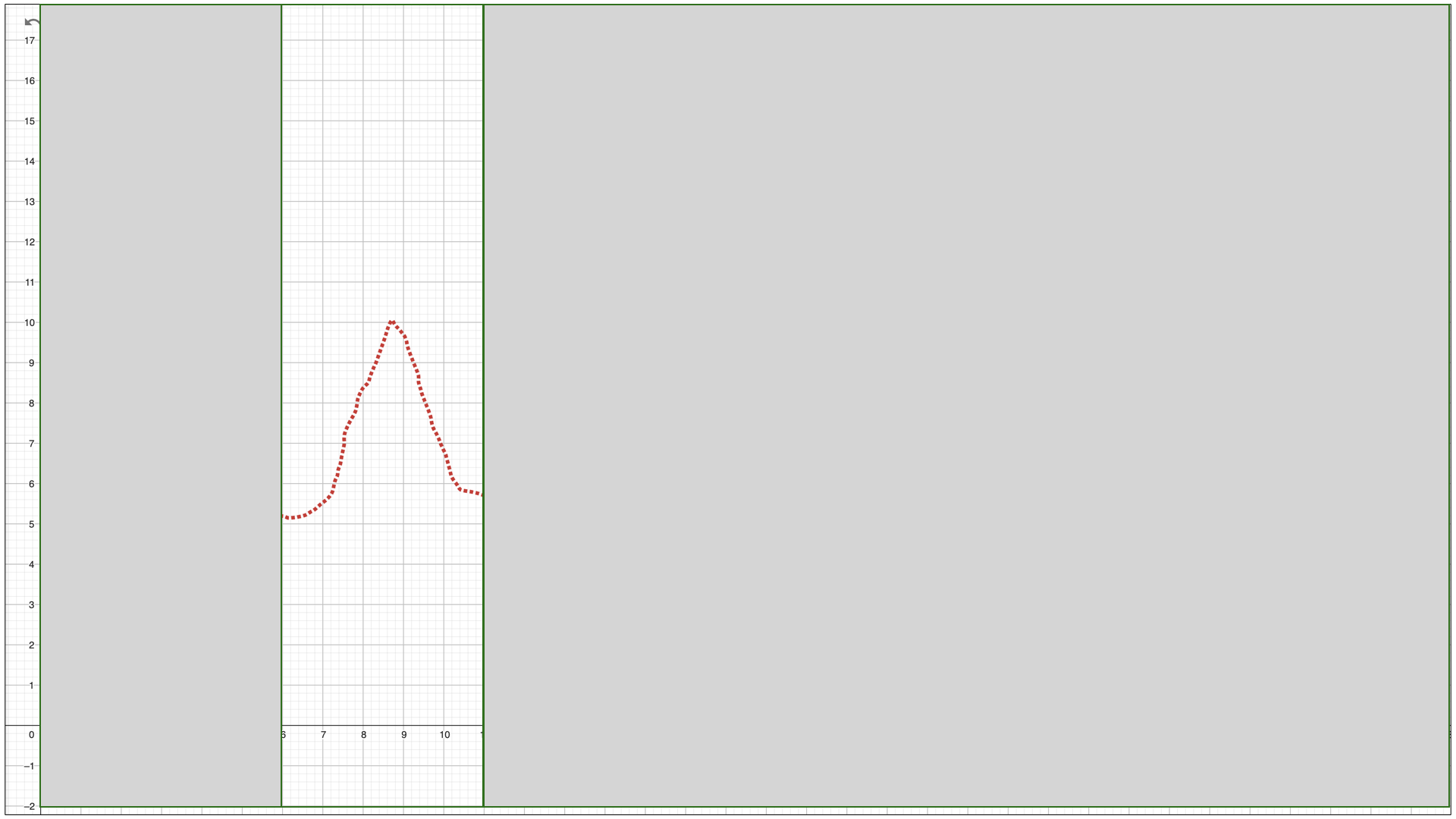
这个时候,虽说这个跳跃有可能确为异常值,但是,也有很大的概率是测量误差或者数据采集错误,很难单凭这一个跳跃就给出任何的判断。
这个时候,我们可以延长检测窗口,如果确实是连续多次跳跃,那这些跳跃成为异常值的概率就很高了:
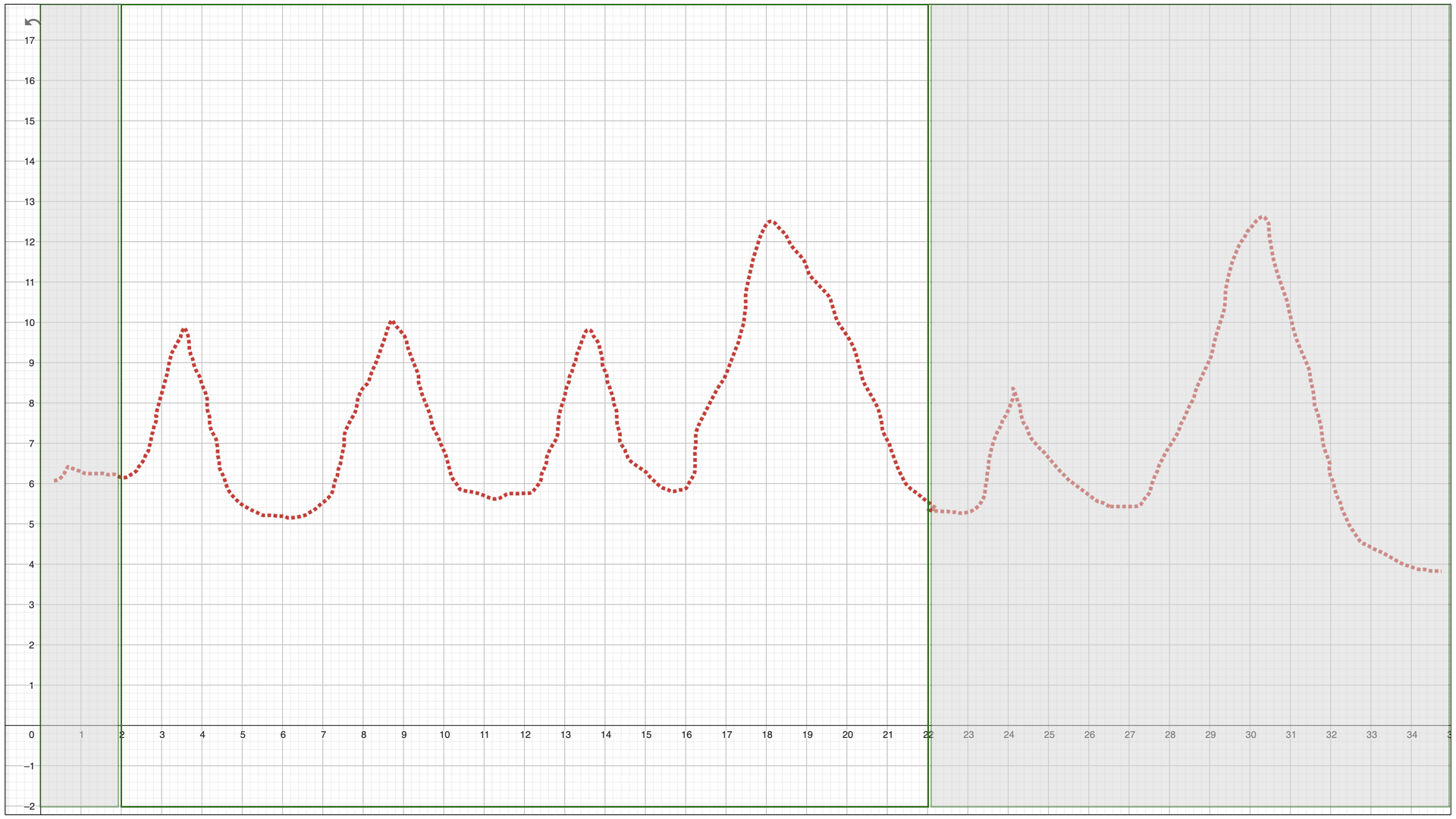
海恩法则
一般来说,如果工况的某个参数代表的是一个连续变化的反馈值,如果出现跳跃,这总是一件不正常的事情。这些很可能就是某个或某些事故或安全事件的前兆。
对跳跃特征,我们可以运用特征统计,比如,每小时,每天。再根据这种特征的统计结果来做一些什么判断。
这就是所谓的海恩法则:每一起严重事故背后,必然有30次轻微事故、和300起未遂先兆、以及1000起事故隐患 。
这个法则强调事故的发生是量的积累的结果。在实际应用中,海恩法则提醒我们在处理事故时,不仅要关注事故本身,还要对同类问题的 “事故征兆”和“事故苗头”进行排查处理,以此防止类似问题的重复发生 。
特征就是征兆,就是苗头。特征统计,就是把这些征兆和苗头就那些量化。当然,这么说的 30、300、和1000次,是一个“积累的量”的概念。
达标检测
除了上面介绍的针对异常的跳跃特征的应用工况场合外,还有另一种跳跃特征应用工况场合,就是检查是否达标,也就是针对正常情况下的使用。
这种情况实际上也很多,比如,冲压、冲击、打击、刺激,等等。比如,某冲压锻造设备,对需要对工件施以多次的快速冲压,这个冲压的动量必须是足够的,次数也是要保证的。
总之,这些特征怎么使用,还是要对具体应用行业的深入理解。
陡升或陡降特征
陡升或陡降类型的特征,有这么几个:
- RSU:无限定陡升
- RUF:限定陡升
- DPD:无限定陡降
- DDF:限定陡降
正向跳跃特征,通俗的说就是 “先跳起来,再落下来”。这个显著的特点就是起跟落必须同时存在,而且还有顺序的要求。
而陡升或陡降特征,通俗的说,就是 “上去了,下不来”,或者 “下来了,上不去”。也就是说,这些特征的共同特点是,变化后一直保持这个变化。
陡升或陡降特征用来对稳定、连续、且本应小幅度变化参数的异常监测。
有些工况场合,数据偶有跳跃,其实并不打紧,对实际工况并没有多少影响,也不会造成什么危害。但如果遇到跳起来且维持,就可能出现大麻烦。比如,某个容器的压力突然增高,且一直维持这个压力,那么,很可能紧接着的就是由于这个高压力维持所带来的一个灾难。
维持特征
维持特类的征有:
- MTN:无限定维持
- MTA:高限维持
- MTB:低限维持
- MBT:高低限维持
维持类特征,通常用来做 “禁区检测”,或者 “达标检测”。
所谓禁区检测,就是这些某些参数存在禁区范围,这个参数的值本不应该在这个区域里待很久。因为如果这个参数值在这个禁区范围内超过一定的时间,就可能出现问题。
比如,压力容器的压力不应该在超过多少兆帕的压力下持续太久,否则会出现安全问题;或者某设备的压力不能低于某个压力太久,否则生成出来的产品会有问题。这是我们比较容易理解的禁区检测。
而成熟检测,机会必须要在某个条件下待多久,才达标。比如,新能源车的电池需要用的碳粉,必须在640°C条件下维持15分钟,再在 380°C条件下维持20分钟,这个碳粉处理才算合格。
波动特征
FLU(波动)就是波动特征。主要是用来检测某个因素的稳定性。
临界特征
临界特征有两个:
- PUA:向上接近峰值点
- PDA:向下接近峰值点
这些特征就是检查当前情况与临界接近的情况。
上述内容我们可以整理一下:

理解这个图,就有助于我们使用好特征检测这个应用。
