- (一)概述
- (二)结构
- (1)便携式设计
- (2)主要构成
- (三)仿真模拟系统
- (1)Simubox
- (2)仿真模型
- (3)Complex 框架
- (四)仿真模型
- (1)基本概念
- (2)仿真脚本文件
- (3)图片文件
- (4)拟音文件
- (五)仿真脚本
- (1)基本概念
- (2)脚本规则
- (3)脚本规范
- (4)保留变量
- (5)变量标签
- (6)周期/顺序
- (7)变量类型
- (8)变量参数
- (9)Simubox 共享计划
- (六)计算模拟变量
- (1)基本概念
- (2)中间变量
- (3)正态模型(N)
- (4)柏松模型(P)
- (5)伯努利模型(B)
- (6)几何模型(G)
- (7)均匀模型(U)
- (8)列表模型(L)
- (9)读数模型(R)
- (10)计算表达式(F)
- (11)回溯变量(H)
- (12)受控变量(C)
- (13)Complex 框架
- ALT消息输出窗口
- Simubox 变量读写
- (七)切换操作
- (八)数据采集
- (1)PLC通讯
- (2)Lua
Mixiot 除了数据模拟应用,还有专门用于仿真模拟的设备,便携式仿真模拟箱。
(一)概述
便携式仿真模拟箱(SimuboxTM),是一个封装在 “箱子” 里面的仿真模拟系统,准确的定义是 “被仿真对象参数的运行(或运动)机理过程数据模拟”。

这里有两个概念:一个是 “被仿真对象”(或者称为 “模拟对象”,简称 “对象”),一个是 “对象参数”(简称参数)。
所谓 “被仿真对象” 或 “模拟对象”,就是我们要模仿的对象。我们可以模仿一些相对简单的设备或者设备组,比如,水泵、水泵房;模仿空压机、空压机站;沼气发电机组、沼气发电站;锅炉、集中供暖锅炉房。我们还可以模拟一些比较复杂的东西,比如,气化热解装置(也就是垃圾焚烧装置),醋酸乙烯酯生产装置,机械式蒸汽在压缩装置(MVR),二段煤气发生装置(城市煤气),污水处理装置,…,等等。Simubox 还可以模拟更加复杂的对象,如,饲料厂、化工厂,热电厂,制药厂等流程工业生产过程。
所谓 “对象的参数”,是指能表示 “被仿真对象” 或 “模拟对象” 运行特征和状态特征的相关参数(也称为模拟对象的参变量)。
不同的 “对象” 类型的 “参数” 是不一样的,如,“水泵” 这个对象的参数不是很多,大体上只有:水泵电机转速、电流,电机频率,水泵出口压力(扬程),流量,等等;再比如,“燃气锅炉” 这个对象的参数大体上有:锅炉燃烧温度、锅炉压力,燃气阀门开度、燃气压力,锅炉排烟温度,锅炉水位,….,等等。但是对一个 “气化热解装置” 或者 “醋酸乙烯酯生产装置” 来说,参数就会非常多了,有生产设备(运行)的,物料的,能耗的(燃气,蒸汽,电),循环的(水、气),生产过程的,产品质量的,排放的,…,等等。
通常仿真对象越复杂,参数就会越多,模拟就越复杂。Simubox 提供了一套统一的模拟方法,可以对超级复杂的工业场景(包括设备运行,生产过程,能耗,排放,等等)进行高仿真度的模拟,以及对模拟对象的控制仿真,为工业物联网的实现进行模拟推演。
(二)结构
模拟箱结构的特点是:
(1)便携式设计
仿真模拟箱使用便携式旅行箱体设计,底部配以滚动滑轮,便于携带。

(2)主要构成
仿真模拟箱由上下两部分构成。上部分主要有仿真计算机,网络交换机,手控调节器、手控开关,启停开关,以及指示灯。

下部分主要有可编程逻辑控制器(PLC),传感器,模数转换模块,和可编程适配器组成。

(三)仿真模拟系统
仿真模拟系统包括四个部分,分别是:硬件部分(在前面已经做了介绍)、基础软件(Simubox)、仿真(对象)模型、和优化控制框架( Complex)。我们可以用一张图来表示整个仿真模拟系统到底是什么:

(1)Simubox
Simubox 是仿真模型箱内置的仿真模拟系统的仿真模拟系统的基础软件,它是仿真模拟系统的核心,决定了仿真模拟的方法和模拟过程。如果把仿真模拟箱比作为一台笔记本电脑,Simubox 就是这台笔记本电脑的操作系统(比如 Windows),没有操作系统,笔记本估计什么也做不了。
(2)仿真模型
仿真模拟系统要仿真模拟什么,并不是 Simubox 说了算,而是由仿真模拟对象模型说了算。如果想要模拟一个 “沼气电站”,就需要有一个 “沼气电站” 的 “仿真模型”;如果想要模拟一个 “醋酸乙烯酯装置”,那也需要有一个 “醋酸乙烯酯装置” 的 “仿真模型”。
在 Simubox 系统中,仿真模型由一系列的文件构成,文件按规定的文件夹目录组织保存,其中最关键的文件,就是 “仿真脚本” 文件,这个文件可以理解为有三个作用:首先是模拟对象的描述和定义,其次是模拟方法定义,最后是模拟过程(控制过程)的定义,本文后面会详细说明。
(3)Complex 框架
仿真模型本身是一个闭环的模拟,这些都通过仿真脚本来实现。我们可以理解为,这是一个能够按我们设计的规则去自我控制的一个自我运行装置。如果没有外部的干涉,这个模型会一直自己的规则运行下去。
Complex 框架是 Simubox 仿真系统之外的一个 “优化控制框架”,或者称为 “控制优化框架”。Complex 并不是一个程序,而是一个程序框架,在这个框架中,可以根据需要去编写程序,对仿真模拟对象的模拟过程进行干涉和影响。
Complex 通常被用在编写一些过程优化程序,能改变或调整原有模拟过程和效果,所以我们也会把 Complex 称为 ”优化控制框架“,就相当于给原有的仿真模型增加了一个新的 ”优化控制器“,这个优化控制器能改变(或改良)原有的控制过程。
(四)仿真模型
(1)基本概念
在 Simubox 仿真模拟系统中,“仿真模型” 包括三个东西:被模拟对象的图片,拟音(音效),和仿真脚本。“三件套” 分别对应三个文件,即 “图片文件”、“拟音(音效)文件”,和 “仿真脚本文件”。
一个仿真模型,必须(也只能)有一个仿真脚本,但是可以有一个或多个图片文件或拟音文件,用来更加逼真模拟不同的工况特征。
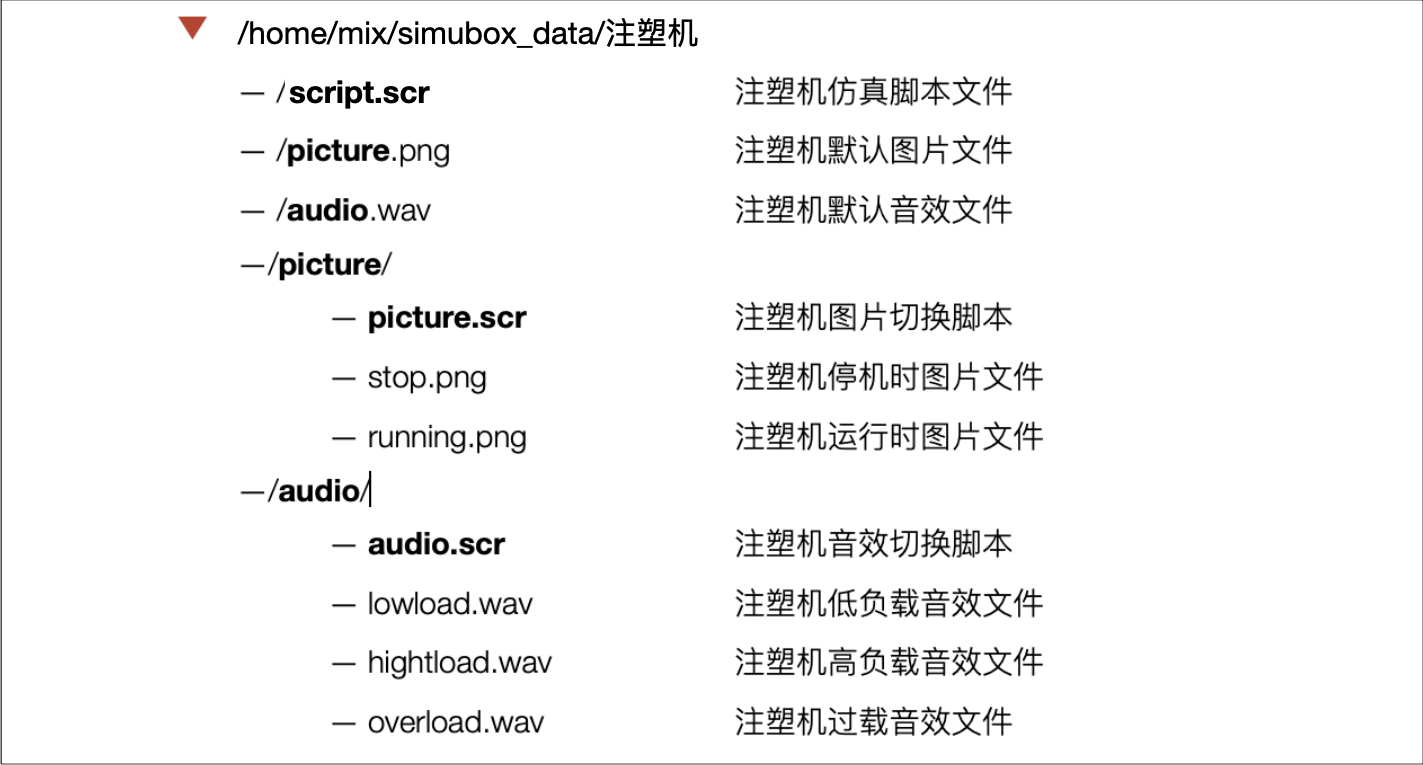
在 SImubox 系统中,一个仿真模型所涉及的文件名和文件组织方式有明确的规定:

Simubox 系统中可以容纳多个仿真模型,它们以平行目录的方式存档在 Simubox 模型系统中:

(2)仿真脚本文件
“仿真脚本(Simubox Script)”。在 Simubox 仿真系统中,无论要模拟什么,无论怎么模拟,都要用一个 “仿真脚本(Simubox Script)” 进行模拟对象定义。虽说仿真模型包括三个东西,但仿真脚本是唯一不能或缺的东西;
仿真脚本文件,是仿真模型中不能缺少的核心文件,是仿真模拟的规则和依据。我们模拟的任何一个仿真对象,都需要为它量身打造一个相应的仿真脚本。仿真脚本文件是一个文本文件,默认文件名为 “script.scr”,并保存在当前模型的文件夹中,当仿真模型被选择时,Simubox 系统会自动加载,并按脚本的仿真规则进行过程模拟。

(3)图片文件
仿真模型中图片文件是必须的。图片文件默认为 “PNG” 格式文件,也支持其他文件格式,如 “JPG”、“BMP” 格式,也支持 “GIF” 动画图片。图片的长宽尺寸大小并没有规定,但图片长宽尺比应为 16:9,如果图片长宽比不是 16:9,图片在加载时会被拉伸,有可能会导致图片变形。
Simubox 可以支持多组图片,也可以使用一个图片。如果只使用一个图片作为默认图片,在模拟过程的自始至终,图片都是同一个,文件名必须是 picture.png,文件位置如图。

如果使用多组图片,可以在模拟过程中,根据不同条件进行图片替换。如,当我们模拟燃气锅炉的时候,锅炉燃烧状态为 “停止” 的时候,用这个图片:

当燃气锅炉燃烧起来的时候,用图片:

如果用的是 GIF 格式的图片,还能显示出燃烧火焰变化的动画效果。
无论是否使用多组图片,默认的图片(文件)都是需要的,而且文件名是规定好的,必须是 picture,扩展名可以是 png、jpg、gif 等等。默认的图片文件将作为仿真对象的默认图片,出现在 Simubox 选择模型的时候。
如果使用多组图片,那就必须要有 picture.scr 文件,这个文件叫 “图片切换脚本(文件)”,用来定义在什么条件下,把默认图片切换成什么。图片切换脚本的写法规定为:
{
“切换条件表达式”:“切换图片文件名”,
“切换条件表达式”:“切换图片文件名”,
……
“切换条件表达式”:“切换图片文件名”
}
我们举个具体的列子来说明:
{
“ $S12 == 0 ”:“stop.png”, (如果模拟变量 S12 = 0 的时候,使用 stop.png)
“ $S12 != 0 ”:“running.jpg” (如果模拟变量 S12 ≠ 0 的时候,使用 running.jpg)
}其中,“S12” 是一个注塑机的模拟变量(这个后面会说明),代表注塑机的启停状态,这个变量在模拟过程中,可能会发生变化,那么,我们通过把这个图片与这个变量来对应。
(4)拟音文件
拟音(音效)文件用来模拟被仿真对象运行时的声音(噪音),让仿真模拟过程更加逼真。音效文件格式默认为 “WAV” 格式,但也支持 “MP3” 格式。

与图片文件的规则一样,Simubox 可以使用一个音效文件,模拟过程只能发出一种声音。Simubox 也支持多个音效文件,切换的规则用 audio.scr 来定义。
规则为:
{
“切换条件表达式”:“切换音效文件名”,
“切换条件表达式”:“切换音效文件名”,
……
“切换条件表达式”:“切换音效文件名”
}切换条件表达式是一个逻辑表达式,可以使用等于、不等于、大于(等于)、小于(等于)、Null 或 None(变量值为空),…,等等。
(五)仿真脚本
(1)基本概念
仿真脚本(Simulation Script)是文本编写的脚本,以文件形式保存在仿真模型文件夹中,默认文件名为 script.scr。
一个仿真对象都对应一个仿真脚本文件,用来定义被模拟对象的参数,按什么规律、规则和特征进行变化,以及被模拟对象参数变化之间的关系。模拟开始前,Simubox 会自动加载仿真脚本,并按仿真脚本为依据进行对象运行过程的模拟。
所模拟对象的参数(参变量)是仿真脚本的 “保留变量”,他们的命名都有固定的规定,最多支持模拟变量个数为 320个,其中,手控调节器变量 6 个,手控开关变量 6 个,故障报警 2 个,温湿度传感器变量 2 个,外部输入模数转换(A/D)变量 16 个,外部输入 PLC 数字量变量 32 个,其余的 256个为计算模拟变量。
(2)脚本规则
仿真脚本由 “行” 组成,每一行描述一个模拟变量。脚本的基本格式为:
[ “变量1”,“变量含义”,“模拟周期”,“变量类型”,“参数1”,“参数2”,“参数3” ]
[ “变量2”,“变量含义”,“模拟周期”,“变量类型”,“参数1”,“参数2”,“参数3” ]
[ “变量3”,“变量含义”,“模拟周期”,“变量类型”,“参数1”,“参数2”,“参数3” ]
….
[ “变量n”,“变量含义”,“模拟周期”,“变量类型”,“参数1”,“参数2”,“参数3” ]SImubox 模拟软件加载仿真脚本后,按脚本的行顺序依次对每一行进行解析,并生成模拟数据。
注:为了书写和阅读方便,本手册中所有涉及的脚本举例,将不出现(西文)双引号,变量后数字也只使用两位。但实际使用中,脚本需要西文双引号,变量数字为三位,否则会被视为无效。
(3)脚本规范
仿真脚本的基本规范可以用下面这个表格来表示:
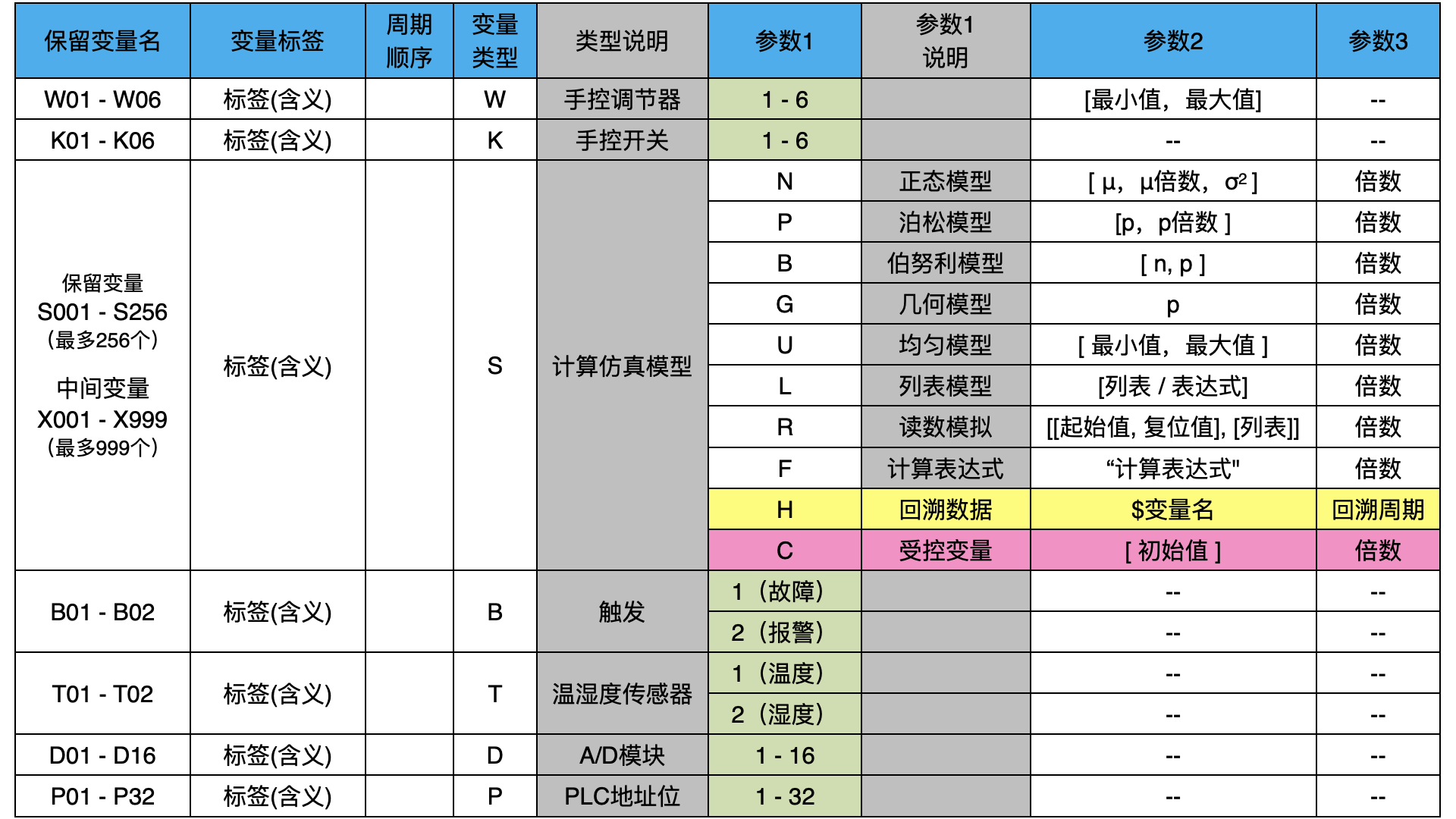
(4)保留变量
仿真脚本允许使用 256个 “保留变量”,是指需要与 PLC 直接交互的(读取或写入),并呈现在 Simubox 模拟程序界面的变量。也就是说只要在脚本中使用了这些变量,那么,这些变量的值就会自动从 PLC 中相应的寄存器中读取,或者写入 PLC 中对应的寄存器,也会显示在模拟软件的显示界面上。
保留变量的命名是确定的,字母必须大写,写法上必须严格按规范要求,否则,Simubox 程序将不会将它写入 PLC,也不会显示在模拟程序界面上。
除了允许有 “保留变量” 外,还允许使用 999个 “非保留变量”,我们称为 “中间变量”。引入中间变量的目的是为了更加方便计算。这是因为有些我们希望模拟的变量,非常复杂,需要通过多次计算而得到。
中间变量,变量名统一用 “X001 ~ X999”,中间变量只是用于仿真系统的计算,并不会写入 PLC。
(5)变量标签
仿真脚本中的变量标签,是这个变量的含义或者名称。比如,变量 “W02” 的变量标签为 “发动机转速”,那么,就代表了 W02 这个变量的含义是 “发动机转速”,这个标签也会呈现在仿真程序的界面上,如下图:

(6)周期/顺序
在仿真脚本你中,“周期/顺序” 是两个含义,第一个含义是 “模拟周期”,在脚本中用数字表示,是指对应模拟变量多久进行一次模拟,单位是秒。模拟周期最小值为 1,最大值不超过 60。该项可以省略,如果省略,默认为 1,也就是每秒钟模拟一次。
固定周期的模拟,就是根据需要对不同的变量确定固定的模拟周期,是最常用的模拟方法。
“周期/顺序” 的另一个含义是 “模拟顺序”,在脚本中的标识方法为 “ [ 顺序条件表达式] ”,当这个表达式逻辑值为真的时候,在下一个周期进行模拟。
我们用一个具体写法为例,说明模拟顺序是怎么回事。
[ K01,变量S01含义, 1, K, 1, (空), (空) ]
[ W02,变量S02含义, 1, W, 1, [0, 100], (空) ]
[ S03,变量S03含义, “<$W02>”, S, F, $W02+10, (空) ] 这段脚本的意思是,变量 K01 和 W02 都是每秒钟模拟一次;而变量 S03 并不是按固定周期来模拟,只是当变量 W02 发生变化的时候才会在下一个模拟周期进行一次模拟,模拟的值为变量 W02 的值加上10。
我们再看一个例子:
[ K01,变量S01含义, 1, K, 1, (空), (空) ]
[ W02,变量S02含义, 1, W, 1, [0, 100], (空) ]
[ S03,变量S03含义, “<$K01>&<$W02>”, S, F, $W02+10, (空) ] 这段脚本的意思是,变量 S03 只有当变量 K01 和 W02 都发生变化的时候,才会在下一个模拟周期进行一次模拟,模拟的值为变量 W02 的值加上10。
模拟顺序表达式用 [ ] 包括,<$变量> 代表某一个变量的变化,用 “ & ” 代表 “与”,用 “ | ” 代表 “或”,当这个表达式的逻辑结果为 “真” 的时候,该变量再进行模拟,如果逻辑结果为 “假”,则该变量的值一直维持不变。
变量的固定周期模拟是最常用的,一般的仿真模拟中,绝大多数的变量都可以使用固定周期模拟。而顺序模拟,一般用于反应模拟对象变量之间会出现 “递延效应”,或者称 “延迟效应” 的时候,这种情况则更精确地模仿了模拟对象的实际效果。比如,我们把一台燃气锅炉的燃气加大,锅炉里面的水温就会升高,但这个升高一定会有一个延迟过程。
如果我们要验证某个模型的优化效果,“模拟顺序” 则是少不了的方法。
(7)变量类型
变量类型是模拟变量的性质,用单个大写字母区分。不同的变量类型代表 Simubox 仿真系统要用不同的方法处理,这个我们会在后面详细说明。
- W 手控调节器类型变量
- K 手控开关类型变量
- S 计算模拟类型变量
- B 触发类型变量,用于触发故障和报警
- T 传感器类型变量(温度湿度传感器)
- D 外部模拟量输入(A/D模块)变量
- P 外部数字量输入(PLC地址)变量
(8)变量参数
仿真脚本的最后三项,分别是参数1、2、3。如果说变量类型是对变量 “质” 的描述,那这三个参数是对变量的 “量” 的描述。参数1,对 W 和 K 类型变量来说,是对应的手控调节器和手控开关的位置,这是一个 “读” 类型的变量,意思是从手控调节器或开关读取的数据。

我们看脚本:
[ W02, 粉碎机转速, 1, W, 2, [15,50 ] , (空) ]
[ K04, 加压泵开关, 1, K, 4, (空) , (空) ]代表的意思是(同上图):
变量 W02,代表的意思是 粉碎机转速,对应的是 第2个手控调节器 的值,调节范围为 15~50;
变量 K04,代表的是 加压泵开关,对应的是 第4个手控开关。
这两个变量,都是每秒钟从手控调节器和手控开关中读取一次,把读取的结果形成 W02 和 K04 变量的值。
我们再看脚本:
[ T01, 环境湿度, 1, T, 1, (空) , (空) ]
[ T02, 环境温度, 1, T, 2, (空) , (空) ]T 类型变量也是 “读变量”,这两行脚本代表的意思是:
变量 T01,代表的意思是 环境湿度,对应的是 第1个温湿度传感器的值,也就是湿度;
变量 T02,代表的意思是 环境温度,对应的是 第2个温湿度传感器的值,也就是温度。

仿真模拟箱中的温湿度传感器,是直接对接到 PLC 中的,所以,我们只需要直接在脚本中声明我们使用这个变量,那么,仿真系统就会自动从 PLC 对应寄存器中把传感器的温度湿度值读出来。
除了手控调节器和开关,温湿度传感器外,仿真模拟箱还支持 16 路外部模拟量的输入,这些模拟量(如,电流、电压)都需要对接到仿真模拟箱的 “模数转换模块”,也就是 A/D 模块。

这些模拟量经过 A/D 模块转换成数字量后,汇集到 PLC 中,分别写到 16 个 PLC 的对应寄存器中。如果我们希望把这些数据也引入模拟过程,则可以用脚本来表示。比如,我们在外部使用了震动传感器,振幅和频率分别对接到第1路和第3路外部输入,那么,脚本可以写成:
[ D01, 振动振幅, 1, D, 1, (空) , (空) ]
[ D03, 震动频率, 1, D, 3, (空) , (空) ]仿真模拟箱还支持 32 路外部数字量直接接到 PLC 中,只要我们明确了那一路输入是什么,就可以用脚本来声明这个变量的使用:
[ P01, 含义, 1, P, 1, (空) , (空) ]
[ P02, 含义, 1, P, 2, (空) , (空) ]仿真模拟箱对外部模拟量和数字量的支持的这个功能非常重要,使得 Simubox 这个仿真模拟平台可以进行更加复杂的模拟,同时也可以用来对接真实设备,对设备进行调优和模型验证。
除了 W,K,T,D,P 这些变量类型,Simubox 仿真系统的关键,就是 S 变量类型了。之所以使用 S 做为变量类型的标识,是因为这类变量数据是通过仿真模拟(Simulaiton)计算而得到的。Simubox 仿真模拟系统,使用了不同的仿真模型来对数据进行模拟,脚本中的参数1,就是对这个变量所使用的仿真模型定义。
每个仿真模型参数的说明,我们放在后面进行专门的讲解。我们先看一个例子,对它们先建立一个初步的印象:

这是我们打算模拟的一个简单的水泵,选择了这么几个关于水泵的参数,分别是:水泵电机开关(K01)、水泵转速(W01),水泵出水压力(S01)、水泵出水流量(S02)。其中,水泵转速 W01 是可以进行手控调节。
对这个水泵,先梳理一下我们的基本的认知:
水泵电机打开,水泵就开始工作,就会有水的进来和出去;如果水泵电机关掉,水泵就不会再有水进出;
水泵电机转得快,水的流量就大,出水口的压力就大;水泵的转速慢,水的流量就越小,出水口的压力就小。
我们设想,把水泵电机的开关,转速,都变成手控。那么,我们就可以这样来写:
[ K01,水泵电机开关, 1,K,1, (空), (空) ]
[ W01,水泵电机转速,1,K,1,[ 500, 2000], (空) ]
[ S01,水泵出口流量, 1,S,N,[ $W01, 0.0032,0.21 ], $K01 ]
[ S02,水泵出口压力, 1,S,N,[ $W01, 0.725,12.5 ], $K01 ]K01,是水泵的开关;K01=1 代表水泵打开,K01=0 代表水泵关掉;
W01,是水泵电机转速的调节,调节范围是 500~2000转/分钟;
S01,是水泵的出口流量,
- 类型是 S,说明这个变量是通过模拟计算出来的;
- 参数1 是 N,说明这个模拟计算是按 “正态” 模型模拟出来的。关于正态模型,我们放在后面详细说明;
- 参数2 是 [ $W01, 0.0032,0.21 ],说明这个正态模型的期望值是 $W01 x 0.0032,离散程度为 0.21。也就是说,流量大概是 转速x0.0032。比如,转速为 1000转/秒 的时候,流量大概为 3.2m3/秒,这个我们称为 “期望值”,因为这个数据是有波动的,实际的数值与期望值是有偏差的,这些偏差的估计(方差)为 0.21。
- 参数3 是 $K01,也就是说,S01(水泵流量)当水泵关掉的时候,流量为零。
- S02,是水泵出口压力,这个值也是计算模拟出来的,符合正态模型。这个值跟水泵电机的转速有关系,如果转速为1000,压力期望值大概是 1000 x 0.725 = 725 KPa 左右,方差值为12.5。同样,当水泵电机关掉的时候,这个值也会为零。
这个水泵的四个参数,两个是手控的,两个是模拟出来的。手控开关可以控制水泵的开关,手控调节器可以用来调整转速,调大或调小。这个模拟我们可以看到,水泵挂掉,啥都没有了。水泵打开,调大转速,水泵出口压力也随之增大,流量也随之增加。
前面这个脚本的四个参数,我们就基本明白了这个模拟是怎么回事儿了,整个水泵的模拟,其实只是用了一个仿真脚本:

那么问题来了,为什么水泵的流量的期望值是转速的 0.0032 倍?为什么是这个模拟要符合 “正态模型” 而不是别的模型?为什么实际水泵流量大小跟期望值的方差是 0.21?为什么水泵压力是转速的 0.725倍?为什么压力方差是 12.5?等等。这就是所谓的模拟机理了,我们要模拟水泵,当然需要明白水泵是怎么回事儿。
智物联将发布一本 《Simubox 仿真脚本编写教程》,除了强化 Simubox Script 规则和原理之外,还会列举大量的实际仿真应用案例,介绍编写仿真脚本的一些技巧和方法。
(9)Simubox 共享计划
我们回到仿真模型的三件套:图片、音效,和仿真脚本,图片和音效实在是太简单了,核心当然就是仿真脚本了。Simubox 系统的仿真脚本非常灵活,而且强大,可以做到非常复杂而且精确的仿真。做的好的仿真脚本,仿真结果与实际设备运行可以说是几乎无异的。
但是,写好一个仿真脚本却不是一件十分容易的事情。
智物联将会主导一个围绕 Simubox 仿真模拟的共享平台(http://simubox.mixiot.top),把做得好的这些不同的仿真模型,分享到这个平台,形成一个 Simubox 的交流圈。这样一来,你熟悉水泵,你就做更专业的水泵模拟;我熟悉锅炉,我就做一个高水平的锅炉模拟;他对污水处理有研究,他就来做污水处理的仿真模型。正所谓,众人拾柴火焰高,我们都能用上高质量的仿真模型。
关于 Simubox 共享的详细资讯,可以在 http://simubox.mixiot.top 上了解,智物联鼓励 Simubox 所有的使用者参与到这个共享平台,互通有无。也鼓励 Simubox 的专业枪手发布自己的杰作,我们大家该出手时就出手,该出钱就出点钱。
智物联也会在共享平台计划中,举办一些仿真竞赛,推动 Simubox 发挥作用。
(六)计算模拟变量
(1)基本概念
前面实际上已经给大家建立了一个模拟计算的基本印象。我们重新回顾一下脚本规则:
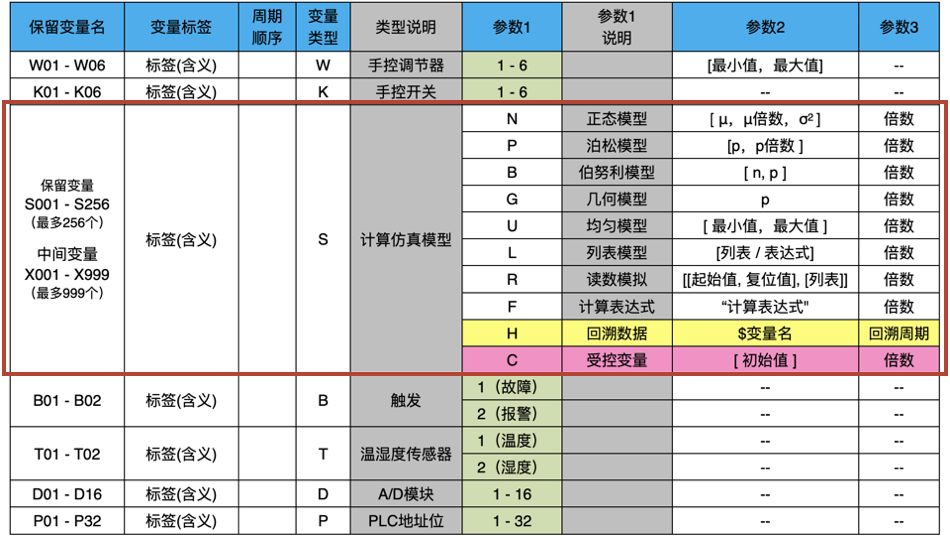
本章节开始逐个说明 S 类型变量,怎么通过计算仿真模拟出来。也会通过实例,说明这些计算模拟怎么使用。对 S 类型变量,参数1 是计算仿真模型;参数2 是表达式,它本身会有个计算结果;参数3,是参数2结果的倍数。
我们留意参数3,这个是一个参数2 模拟计算结果的一个倍数。所以,对 S 类变量而言,这个变量的值是:
S变量的值 = 参数2结果 x 参数3
通常,参数3 会使用一些开关量,也就是 $K,这个值只能是 0(关)或者是1(开)。当然也可以用其他的,常数,$Kxx,或者 $Wxx,$Sxx,这些我们要灵活运用。这里需要说明的是,Simubox 的保留变量最多支持 256个,对一般的模拟应该是足够的。
(2)中间变量
前面的章节中介绍过,如果脚本中使用的是保留变量,那这些变量会直接对应到 PLC 和 Simubox UI 上。但除了保留变量,我们还可以使用 “非保留变量”,也就是所谓的 “中间变量”。中间变量虽然出现在脚本中,但是这些变量既不会直接写到 PLC 寄存器中,也不会显示在 Simubox UI 上。
我们先看一个简单的场景:
这是一个简单的电路,有一个 “基本恒定” 的 36V 供电。W01 和 W02 是两个范围不同的可变电阻。现在,我们来模拟 S01、S02、S03(电压)和 S04(电流)。
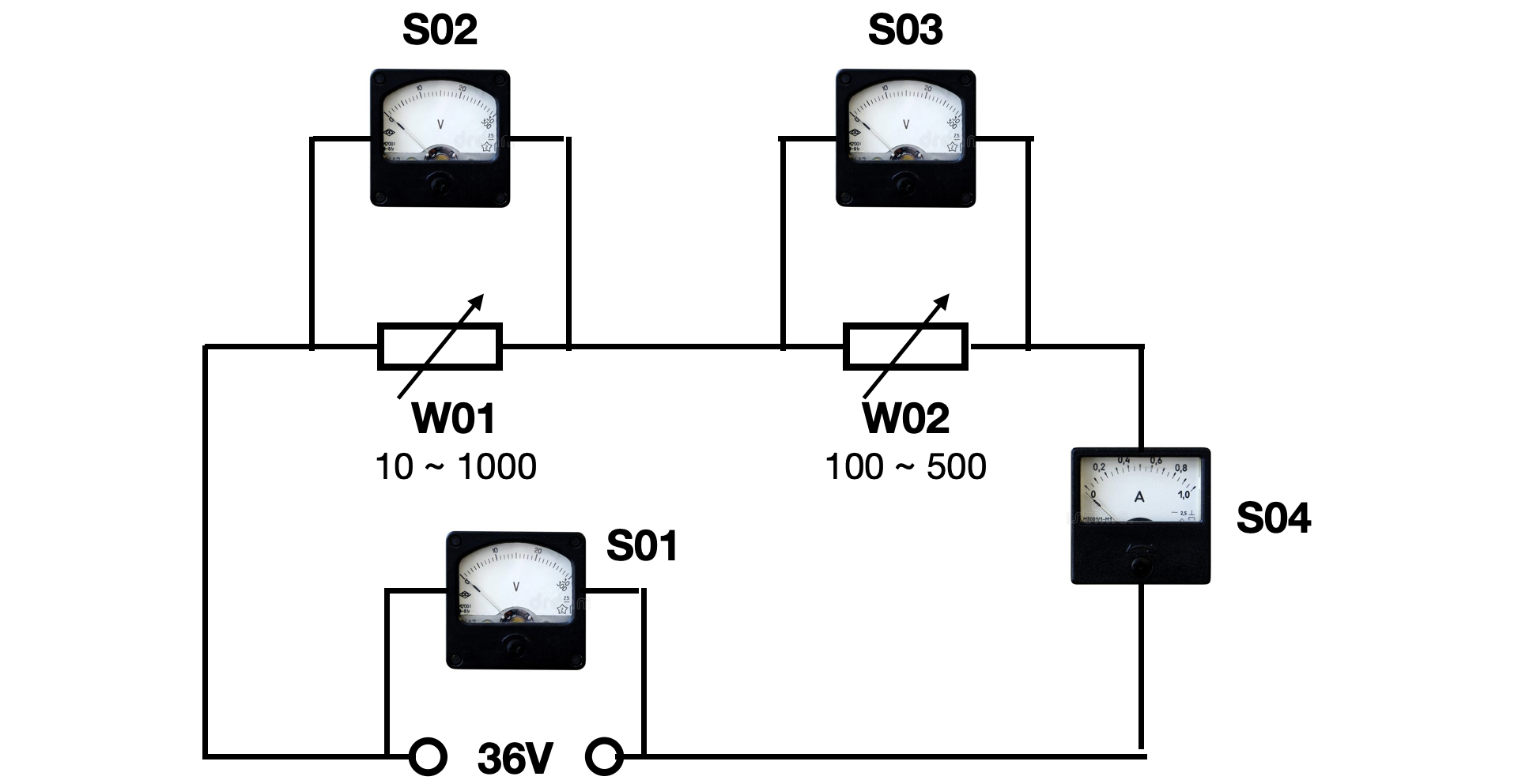
我们先把两个可变电阻模拟出来,脚本如下:
[ W01,可变电阻1#,1,W,1,[ 10, 1000 ],(空) ]
[ W02,可变电阻2#,1,W,2,[ 100, 500 ],(空) ]我们现在来模拟 S01,可以这样写:
[ S01,供电电压, 1,S,N,[ 36, 1,0.35 ],1 ]这个的意思是说,虽然提供的是 36V 的 “基本恒定” 的供电,但免不了供电电压会有波动,这个波动都是围绕 36V 来波动的。
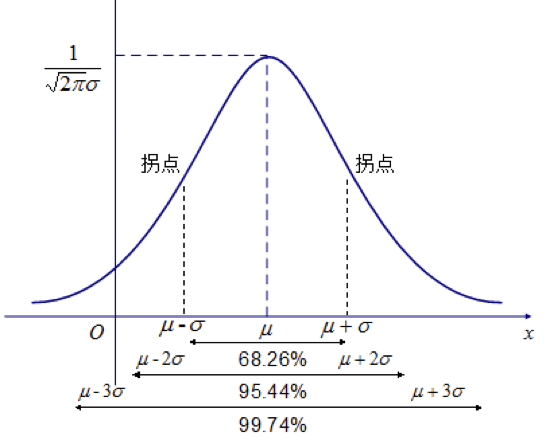
方差我们定在 0.35,说明我们模拟的实际供电电压,有 68.26% 的概率会在 35.65~36.35 范围之间;有 95.44% 的概率会在 35.30~36.70 范围之间;有 99.74% 的概率会在 34.95~37.05 范围之间。那这个就基本上满足我们的设想。
我们再看 S04,电流的模拟,我们可以使用一个中间变量,先算出两个串联的电阻的总电阻:
[ X01,中间变量(总电阻), 1,S,F,[ $W01 + $W02 ],1 ]再用一个中间变量,根据欧姆定律把理论计算的电流算出来:
[ X02,中间变量(总电流), 1,S,F,[ $S01 / $X01 ],1 ]那么,电流 S04 就可以这样来模拟:
[ S04,电路电流, 1,S,N,[ $X02, 1,0.01 ],1 ]在两个中间变量的脚本中,F 是函数计算类型。
有了电流 S04 模拟出来之后,那么,我们也可以用这个电流的值,和电阻的值,用欧姆定律计算出 S02 和 S03,同样,我们也需要用到两个中间变量:
[ X03,中间变量(S01电压), 1,S,F,[ $S04 * $W01 ],1 ]
[ X04,中间变量(S02电压), 1,S,F,[ $S04 * $W02 ],1 ]然后,再把 S02,S03 模拟出来:
[ S02,电压1, 1, S, N, [ $X03, 1,0.01 ], 1 ]
[ S04,电压2, 1, S, N, [ $X04, 1,0.01 ], 1 ]我们把整个电路的模拟的脚本归拢到一起,整个脚本是这样的:
[ W01,可变电阻1#, 1,W,1,[ 10, 1000 ], (空) ]
[ W02,可变电阻2#, 1,W,2,[ 100, 500 ], (空) ]
[ S01, 供电电压, 1,S, N,[ 36, 1,0.35 ], 1 ]
[ X01, 中间变量(总电阻), 1,S, F,[ $W01 + $W02 ] 1 ]
[ X02, 中间变量(总电流), 1,S, F,[ $S01 / $X01 ], 1 ]
[ S04, 电路电流, 1,S, N,[ $X02, 1,0.01 ], 1 ]
[ X03, 中间变量(S01电压),1,S, F,[ $S04 * $W01 ], 1 ]
[ X04, 中间变量(S02电压),1,S, F,[ $S04 * $W02 ], 1 ]
[ S02, 电压1, 1,S, N,[ $X03, 1,0.01 ], 1 ]
[ S04, 电压2, 1,S, N,[ $X04, 1,0.01 ], 1 ]红色的部分,就是我们用到的中间变量。中间变量的使用,目的是方便我们的计算。
这里有个非常重要的地方,就是这个脚本的顺序。前面介绍过的,Simubox 仿真系统加载仿真脚本后,是逐行进行解析和计算的,这是一个规则。如果我们把这个顺序写颠倒了,那么,这一行的计算就要用到后面的变量值,那这一行的模拟计算就会出错。
我们看到参数3,都是1,这是因为不需要额外的倍数。如果我们把电路改一下,加一个开关:
那整个脚本就可以变成这样:
[ K01,电路开关, 1,K,1, (空), (空) ] 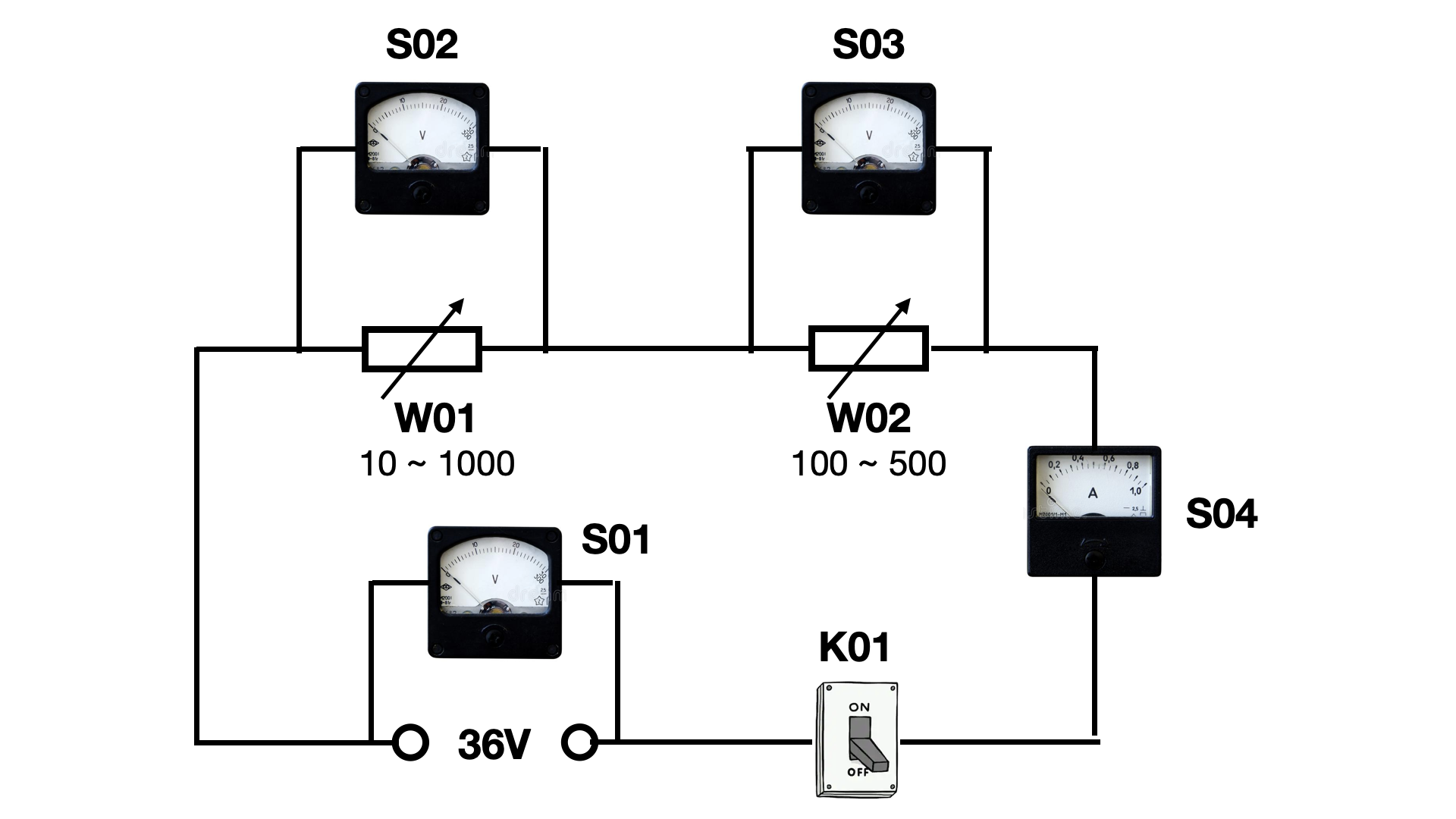
[ W01,可变电阻1#, 1,W,1,[ 10, 1000 ], (空) ]
[ W02,可变电阻2#, 1,W,2,[ 100, 500 ], (空) ]
[ S01, 供电电压, 1,S, N,[ 36, 1,0.35 ], 1 ]
[ X01, 中间变量(总电阻), 1,S, F,[ $W01 + $W02 ], 1 ]
[ X02, 中间变量(总电流), 1,S, F,[ $S01 / $X01 ], 1 ]
[ S04, 电路电流, 1,S, N,[ $X02, 1,0.01 ], $K01 ]
[ X03, 中间变量(S01电压),1,S, F,[ $S04 * $W01 ], 1 ]
[ X04, 中间变量(S02电压),1,S, F,[ $S04 * $W02 ], 1 ]
[ S02, 电压1, 1,S, N,[ $X03, 1,0.01 ], $K01 ]
[ S04, 电压2, 1,S, N,[ $X04, 1,0.01 ], $K01 ] 当开关短路的时候,除了 S01 还有,别的都变成了 0。中间变量使用 $K01 也行,不使用也行,这都不影响模拟结果。
(3)正态模型(N)
前面的举例中,都用到了正态模型。正态模型(Normal Model)密度函数为:
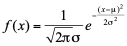
图示为:
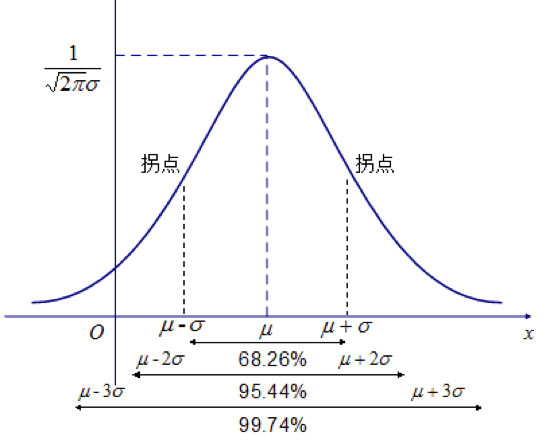
正态分布是最常用的概率分布模型,绝大多数情况下,我们都可以使用这个模型来模拟数据。我们在配置脚本的时候,使用两个关键参数,一个是期望值,一个是方差。
脚本形式为:
[ X, 变量含义, 周期,S, N,[ 期望值, 期望值倍数,方差 ], 倍数 ](4)柏松模型(P)
柏松模型(Poisson’s Model)密度函数为:
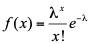
离散条件下表达为:
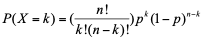
图示为:
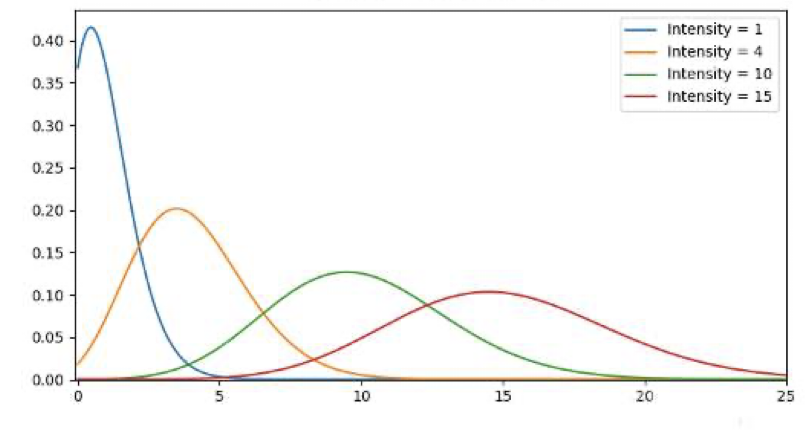
脚本形式为:
[ X, 变量含义, 模拟周期,S, P,[ p, p 倍数 ], 倍数 ](5)伯努利模型(B)
伯努利模型(Bernoulli’s Model)可以描述为:


脚本形式为:
[ X, 变量含义, 模拟周期,S, B,[ n,p ],倍数 ](6)几何模型(G)
几何模型(Geometric Model)可以描述为:

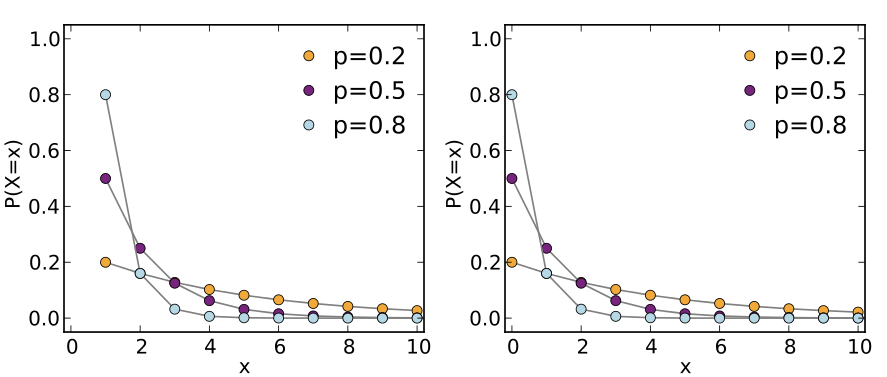
脚本形式为:
[ X, 变量含义, 模拟周期,S, G,[ p ], 倍数 ](7)均匀模型(U)
均匀模型(Uniform Model),也是最常用的模型之一,用于模拟一些基本是会均匀分布在某个区间范围的变量。
脚本形式为:
[ X, 变量含义, 模拟周期,S, U,[ 最小值, 最大值 ],倍数 ]这个变量 X 的模拟的结果是,会在 最小值~最大者 之间产生一个随机数。这个区间产生的随机数的概率是均匀的。
最小值和最大值,可以是常数,也可以是变量。
(8)列表模型(L)
列表模型(List Model)是指确定一个列表,从列表项中随机选择某一项。
脚本形式为:
[ X, 变量含义, 模拟周期,S, L,[ 列表 ], 倍数 ]其中,列表可以是确定的常数,也可以包含变量。
如:
[ X, 变量含义, 模拟周期,S, L,[ 1,2,3,4,5 ], 倍数 ]或者
[ X, 变量含义, 模拟周期,S, L,[ 1,2,3,$S12,$S23 ], 倍数 ](9)读数模型(R)
读数模型(Registration Model)是指对某些仪表的模拟。
脚本形式为:
[ X, 变量含义, 模拟周期,S, R,[ [ 起始值,复位值], [ 变量或列表 ] ],倍数 ]举个例子来解释读数模型。
我们看这样一个脚本片段:
[ S12, 每秒用电量, 1,S, N,[ 3,1,0.2 ] ], 倍数 ]
[ S13, 电表读数, 1,S, R,[ [ 45678,99999], [ $S12 ] ],倍数 ]这里有两个变量,S12 是瞬间(每一秒钟)的耗电量,每秒钟用电量3度左右;而 S13 是电表的读数,这个电表的读数是从 45678 开始累积,累计的量是 S12,也就是每秒钟的用电。
我们还可以这样,
[ S12, 每秒用电量, 1,S, N,[ 3,1,0.2 ] , 倍数 ]
[ X01, 中间变量, 10,S, F, [ integrate(#S12, 10) ] , 倍数 ]
[ S13, 电表读数, 10,S, R,[ [ 45678,99999], [ $X01] ], 倍数 ]在这里,电表读数(S13)并不是每秒钟都累加,而是10秒钟累加一次,每次累加的量,是每秒钟用电量的积分。
无论上述的电表读数 S13 是何种方式去计算,这个读数从 45678 开始,等这个读数到了 99999 的时候,就会复位归零,继续从头开始。
关于读数如何使用,可以参考 Mixiot 统计计算相关读数转用量相关文稿。
(10)计算表达式(F)
计算表达式(函数和运算符)的基本规则是:
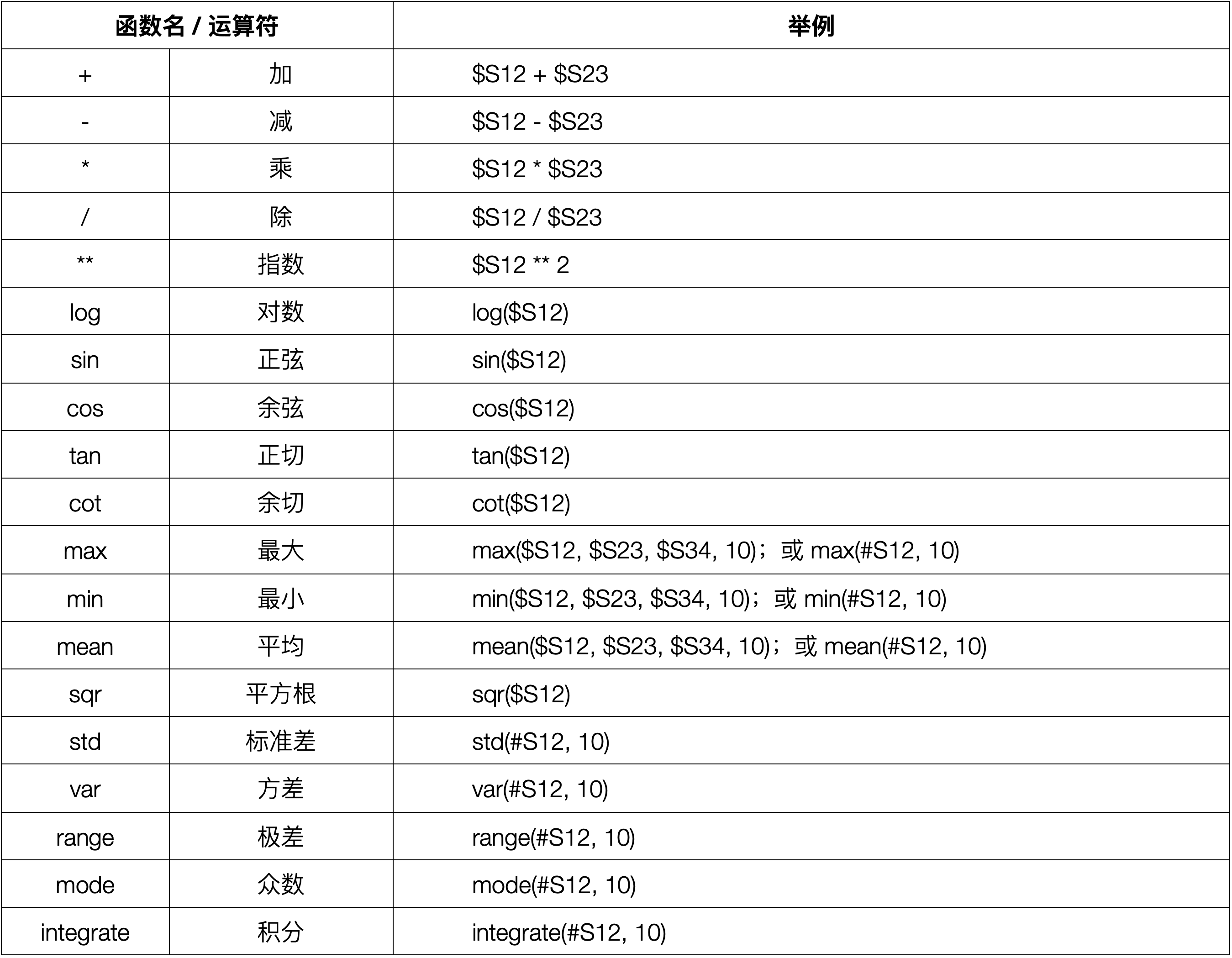
这里面,变量 Sxx 前面有两个标识符,一个是 $,一个是#,含义是不一样的,max($S12, 10),是变量 S12 与数字 10 两者中的最大者;而 max(#S12, 10) 的含义是,变量 S12 最后10个数据中的最大者。
逻辑条件表达式
运算表达式中,也支持条件表达式,写法为:
[ 变量,变量含义,周期/顺序,S,F,“值1 if 条件表达式 else 值2 ”,参数三 ]意思是,如果 条件表达式 成立(为 “真”),则变量为 “值1”,否则(为 “假”)变量为 “值2”。
F 类条件表达式中支持 $变量(宏变量),==(等于)、!=(不等于)、>(大于)、>=(大于等于)、<(小于)、<=(小于等于),以及 Null / None(空值),and / or 或者 & / I (与/或)和 True / False(真/假)。
我们看这几行脚本:
[ K01,变量含义, 1, K,1, (空), (空) ]
[ W01,变量含义, 1, W,1,(空), (空) ]
[ W02,变量含义, 1, W,2,(空), (空) ]
[ S12,变量含义, 1, S,N,[100, 1, 0.25 ], $K01 ]
[ S13,变量含义, 1, S,F, “$W01 if $K01 == 0 else $W02” , (空) ]
[ S14,变量含义, 1, S,F, “$S12 if $S12 <= $S12 else $S13” , (空) ]
[ S15,变量含义, <$S13>, S,F, “$S13 if $W01 != $W02 else $S14” ,(空) ]这几行脚本都必将容易理解,就不多解释了。
这类总结说一下有关 “逻辑条件表达式” 的问题。Simubox 涉及到 “逻辑条件表达式” 的地方有四处,分别是 “图片切换脚本”、“音效切换脚本”、以及 Simubox 仿真脚本中的 “模拟周期/顺序” 和 “F类模拟变量计算表达式”,但它们的逻辑条件表达式能支持的内容不尽相同。
我们可以用一个表来表示:
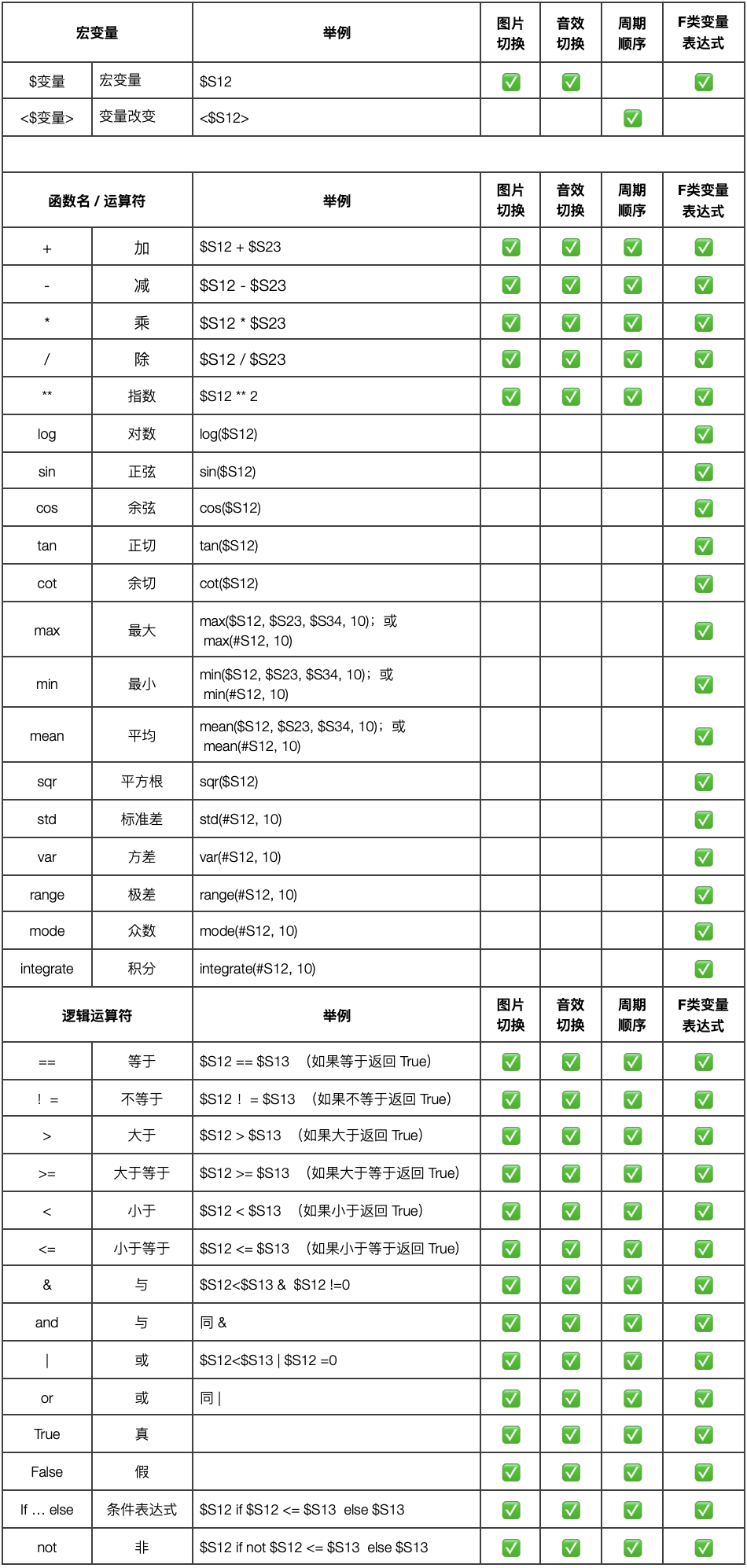
Simubox 表达式基本的规则是:
- 宏变量 “ $变量 ” 代表该变量的值;
- 宏变量 “ #变量,n” 代表变量最近 n 个值,n 范围为 1~ 60;
- <$变量> 是一个逻辑值,True(真)或者是 False(假)。如果 $变量 本周期的值与上一周期改变,则 <$变量> 为 True,否则为 False;
- 表达式函数,及表达式规则,兼容 Python 函数和表达式规则。
(11)回溯变量(H)
仿真脚本的 H 类变量称为 “回溯变量”,用来获取某个变量之前 1~59 个周期的数据,写法为:
[ 变量,变量含义,周期/顺序,S,H,“[ $变量,-1 ~ -59 ]”,参数三(倍数) ]如,
[ S12,变量含义,1,S,H,“[ $S06,-1 ]”,(空) ]代表 S12 这个变量,是 S06 变量的前一个值。
回溯变量(H)经常用于需要考虑递延效应的仿真场合。我们来看一组脚本:
[ X06,变量含义,1, S,H,“[ $S06,-1 ]”,(空) ]
[ X07,变量含义,1, S,H,“[ $S07,-1 ]”,(空) ]
[ S12,变量含义, “ <$S06> | <$S07>”, S,F,“$X06 * $X07”,(空) ]上面的这个脚本中,S12 这个变量,是在 S06 和 S07 其中一个发生变化后才会变化,而变化的值,是 S06 和 S07 的前一个值的乘积,而不是当前的值。
(12)受控变量(C)
仿真脚本的模拟计算的变量类型中,C 类变量称为 “受控变量”,准确的说,应该叫 “外部可控” 变量,它也是由仿真程序计算产生,格式为:
[ 变量, 变量含义, 1, S, C, [ 初始值 ], (空) ]这个脚本在仿真模拟程序运行后,变量只按 “参数二”(初始值) 产生一次。产生初始值后,Simubox 仿真程序会释放对 C类变量的控制权,并不再去对这个数字做任何新的模拟,该变量就可以由外部(第三方)程序控制。
我们看一个脚本:
[ S12, 变量含义, 1,S,U,[ 1.5, 1.8 ], (空) ]
[ S23, 变量含义, 3,S,N,[ 100, 1, 1.5 ], (空) ]这两行脚本我们应该已经非常熟悉了,S12 是在按均匀分布概率大小,在 1.5 和 1.8 之间,每秒钟产生一个随机数;而 S23 则是以100为期望值,1.5为方差值,按正态分布概率,每3秒钟产生一个随机数。请注意的是,上述的随机数是按制定的周期(1秒或3秒)产生一次,连续不断。
我们再看一行脚本:
[ S12, 变量含义, 1, S,U,[ 1.5, 1.8 ], (空) ]
[ S23, 变量含义, 3, S,N,[ 100, 1,1.5 ], (空) ]
[ S51, 变量含义, (空), S,C,[ 35 ], (空) ]
[ S52, 变量含义, (空), S,C,[ 2.64 ], (空) ]
[ S53, 变量含义, (空), S,C,[ 123.45 ], (空) ]
[ S61, 变量含义, 1, S,N,[ $S51,1,0.1 ], (空) ]
[ S62, 变量含义, 1, S,N,[ $S52,1,0.1 ], (空) ]
[ S63, 变量含义, 1, S,N,[ $S53,1,0.1 ], (空) ]变量 S51、S52、S53 就是三个所谓的 “受控变量”,在 Simubox 程序运行的时候,这三个变量只产生一次,这个变量产生这一次的值大小,分别是 S51=35,S52=2.64,S53=123.45。在此之后,仿真程序便不再去理会这三个变量了,如果没有外部的干涉,这三个变量的值就一直不变。
那么,这三个 C 的变量不再由 Simubox 仿真程序去控制了(因为不再去对这个变量进行模拟计算),其实就是交给 Complex 的算法模型去控制了,也就是说,这几个值是由 Complex 程序去改写了,S61,S62,S63 就会跟着发生变化;如果 Complex 算法不去改变,那就会一直维持之前的样子。

Complex 算法模型要算出个什么目的,这个是由它自己决定的,Simubox 则该干嘛干嘛,该怎么干怎么干,并不会因为有 Complex 的存在而改变什么,只是有些变量只是按脚本的要求,产生一次初始化的 S/C 变量值,仅此而已。
(13)Complex 框架
前面介绍过,Complex 是 Simubox 仿真体系的一个第三方程序框架。这个程序框架是为了允许第三方编写自己的 “控制协同” 或者 “控制优化” 算法程序(算法模型),对已有仿真模型的进行原有 “自我控制” 基础上的优化。
Complex 程序框架提供了三个功能,分别是:
(1)提供了算法程序对 Simubox ALT消息输出窗口;
(2)提供了算法程序对 Simubox 仿真模型的变量组的读取方法(Simubox Retrieve);
(3)提供了算法程序对 Simubox 仿真模型的 C 类受控变量的操控方法(Simubox );
ALT消息输出窗口
Complex 框架下的算法程序,一般来说都是以计算为主,并无需有自己的 UI,但可以把相关文本消息通过 Complex 框架上的 ALT消息输出窗口查看。也就是说,Simubox 并不关心算法模型程序怎么写,但提供了 Complex 消息输出的接口和窗口,在 Simubox 主界面上可以打开这个窗口,看到算法程序输出的消息。
Simubox 的主界面上,有一个 ALT 输出(UI 切换)标记,如图:
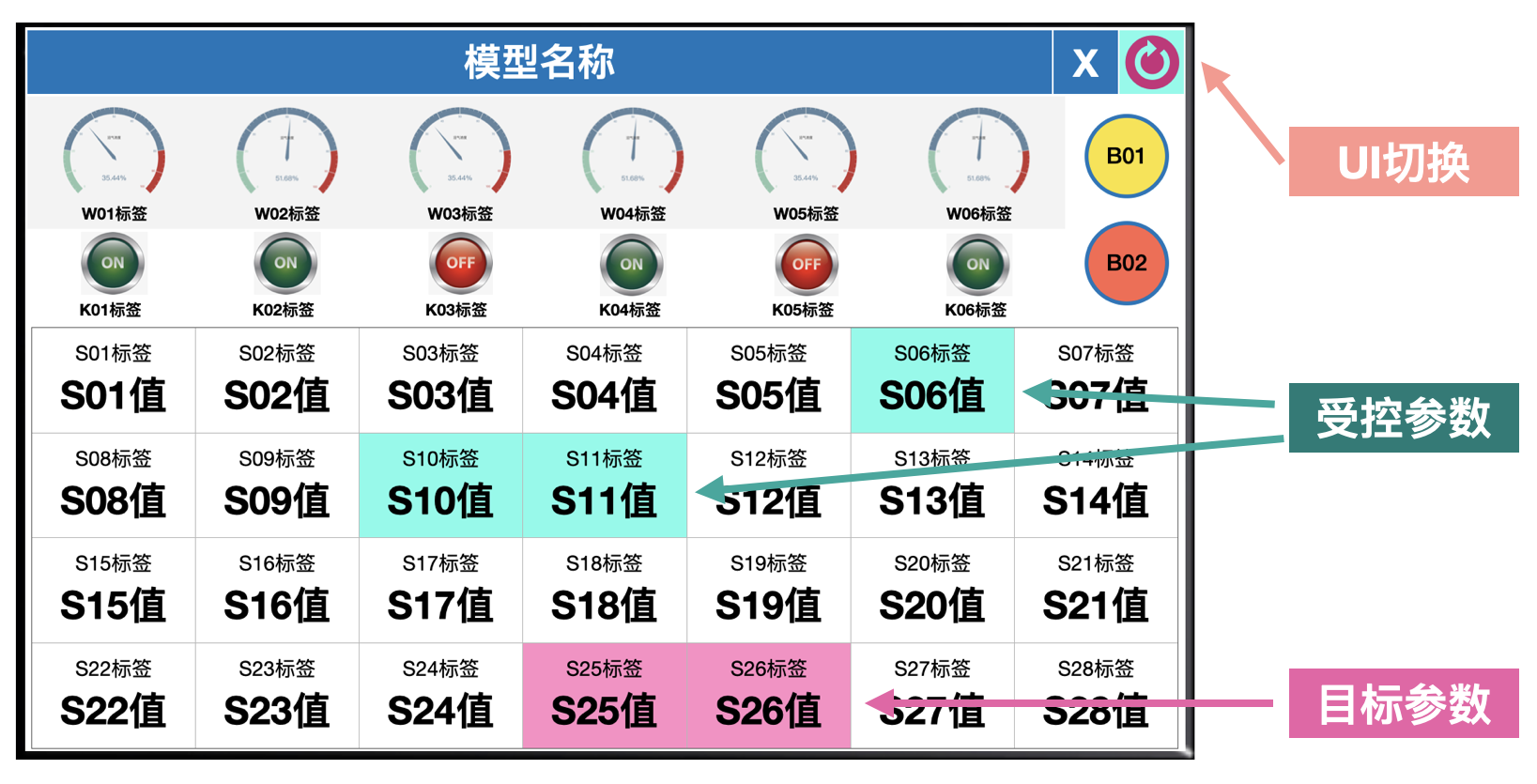
在 Simubox 上点击 ALT输出 按钮,就可以切换到 ALT消息窗口:

Simubox 提供的 ALT消息输出接口为 Socket,以 Python 程序为例,使用方法为:

无论算法程序用什么方式编程,只要使用这个 Socket,就可以把需要输出的消息推送到 ALT消息窗口,通过 ALT输出 按钮可以切换到这个窗口,查看算法程序输出的消息。
Simubox 变量读写
Complex 框架为算法程序提供了一个标准的 IPC 方法,可以对当前仿真模型变量(值)读写操作。下面以 Python 为例,我们逐个说明这些方法:
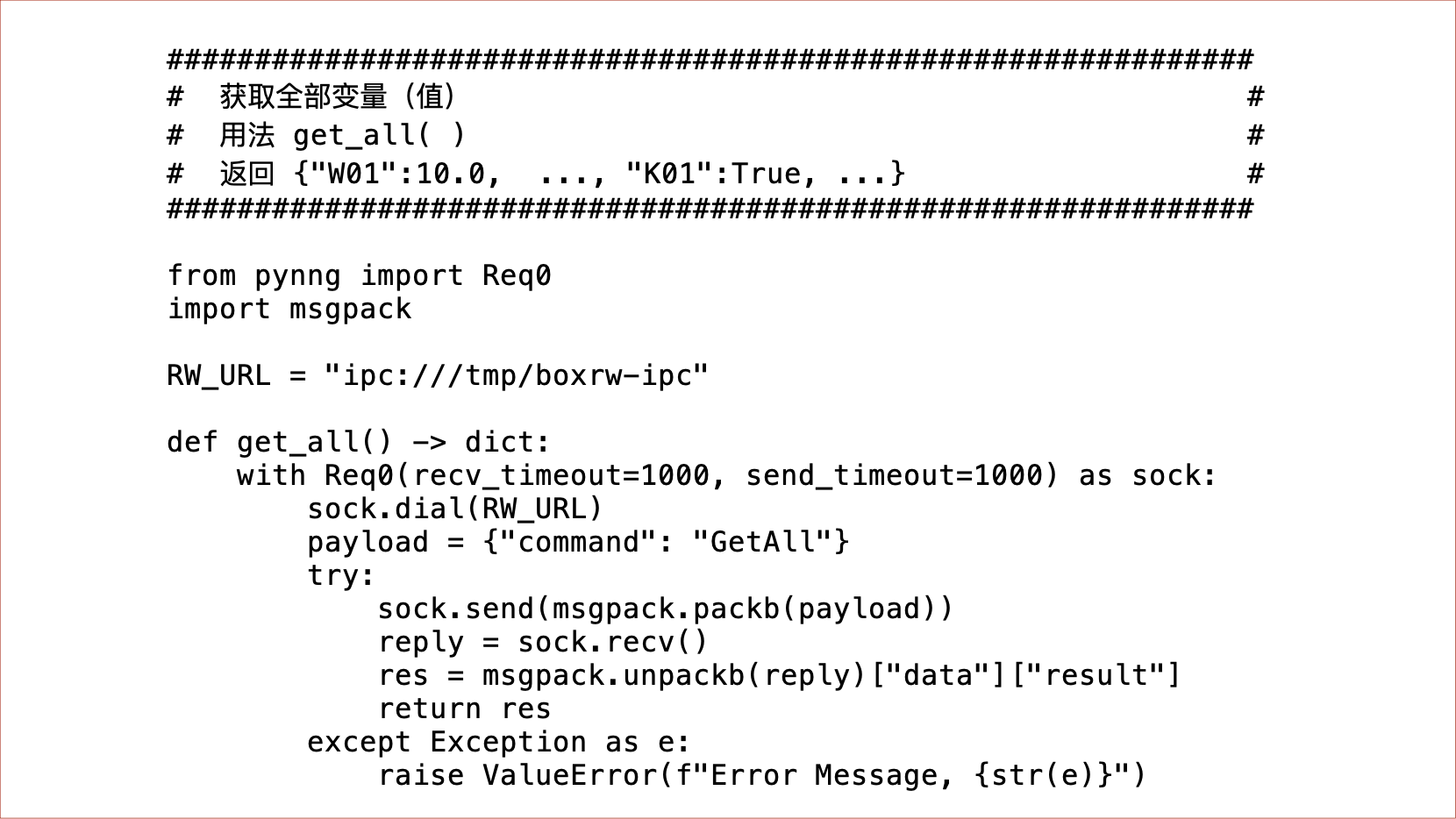
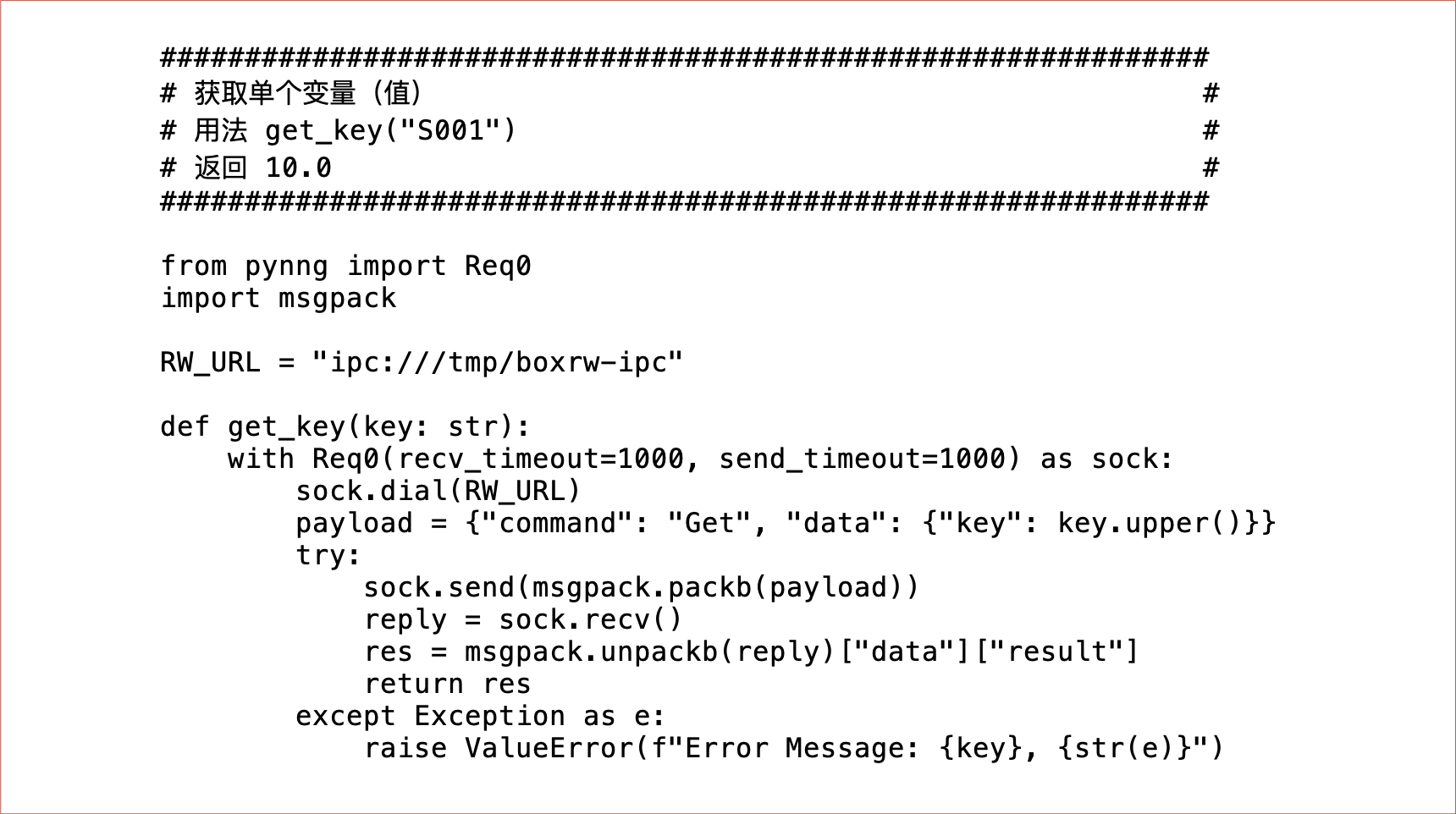
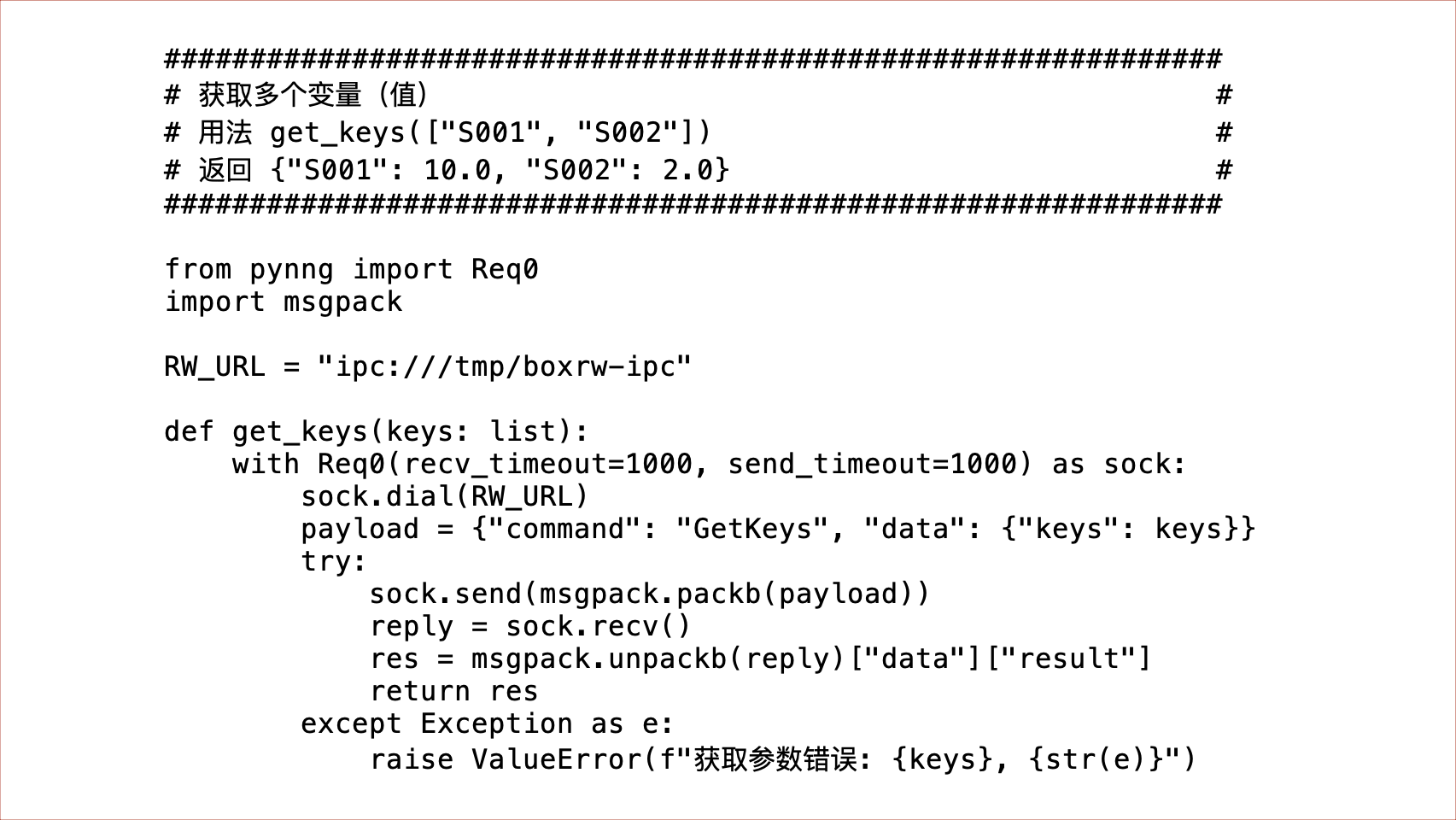
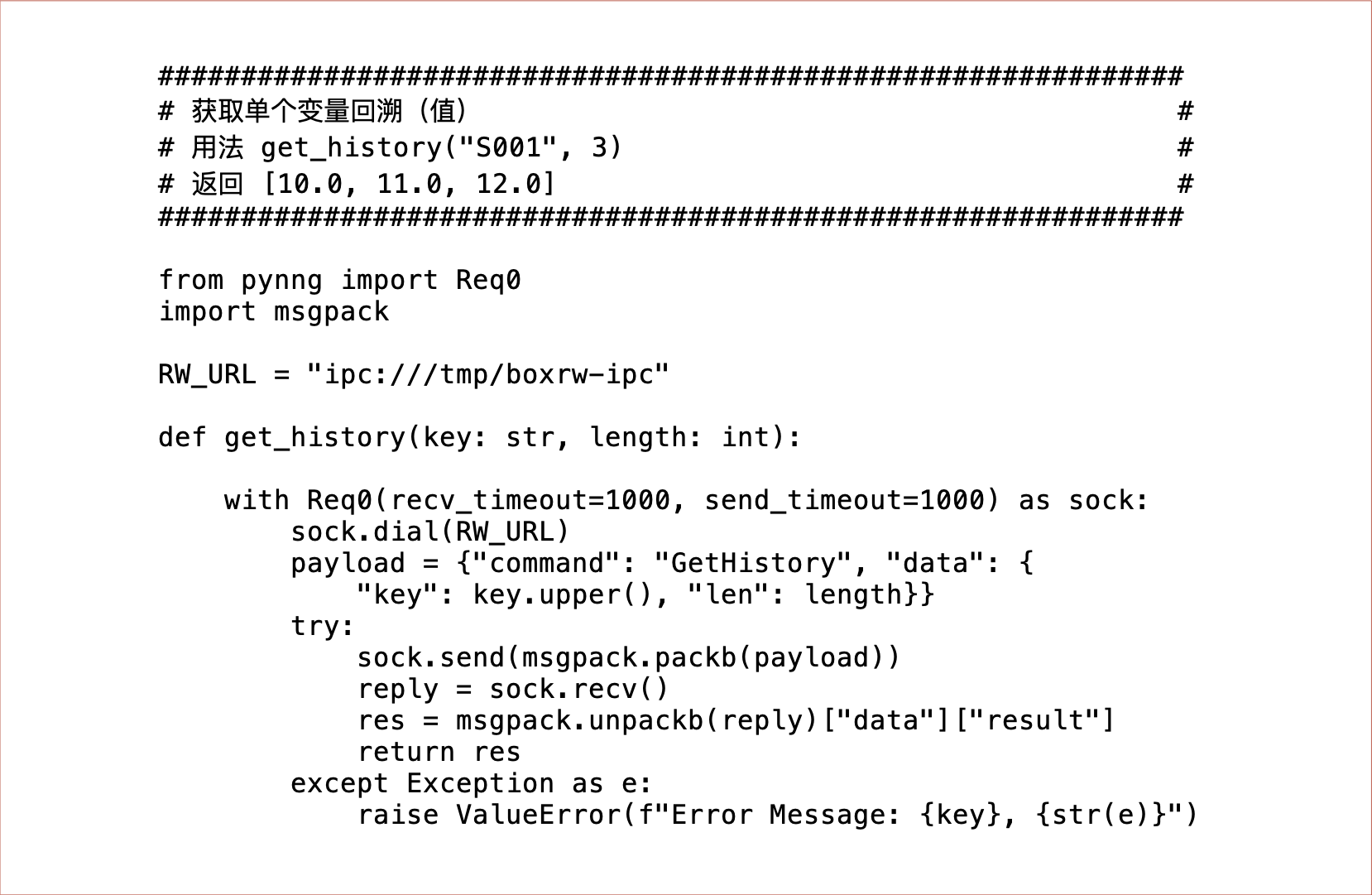
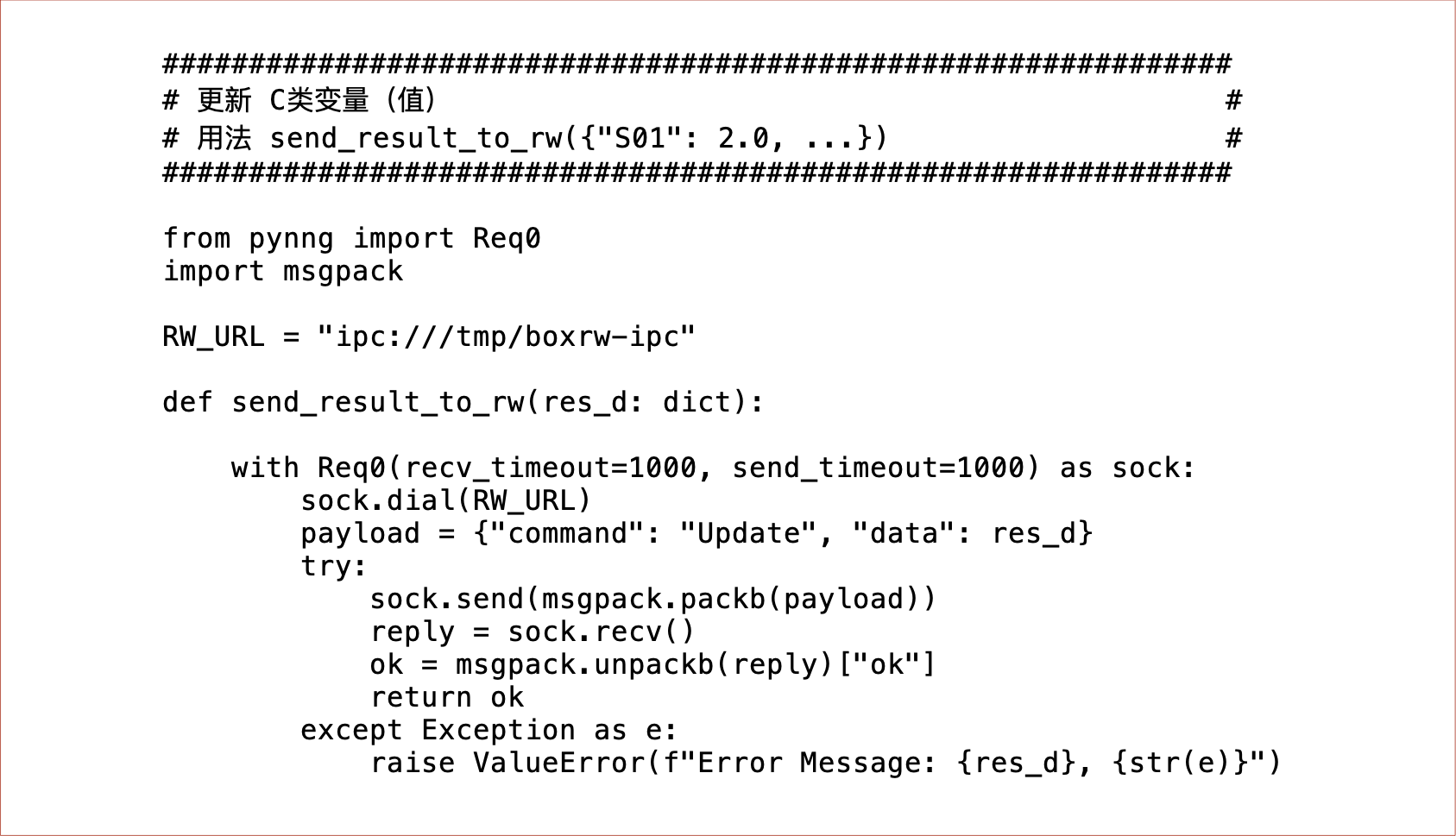
几个地方说明如下:
获取单个变量回溯(值)。变量回溯(值)是指获取某个变量前 1 ~ 59个周期的值。Simubox 系统对仿真变量的值仅保存最近 60 个模拟周期的数值(包括当前最新的变量值),所以,代码中的 len(回溯长度 length)的许可范围是 1 ~ 59,返回的是最近 len 回溯长度的全部变量(值);
更新 C类变量。对 Simubox 仿真脚本中的 C类变量(受控变量),算法程序可以对它们进行更新(改写),该用法只能对 C 类受控变量进行更新(改写),任何试图对其他非 C类变量的更新(改写)都将导致错误消息的返回,更新(改写)不会成功。
(七)切换操作
模拟箱通电启动后,Simubox 模拟系统就会自动运行。可以使用 Ctrl+Alt+F2 切换到 Linux 桌面。

可以使用 Ctrl+Alt+F3 切换到 Linux 命令终端。

(八)数据采集
(1)PLC通讯
Simubox 所有数据都集中在 PLC 里面了,Simubox PLC除了支持常规的 RS-485 Modbus 通讯还支持 Modbus TCP 的通讯。PLC 的 TCP 通讯地址是统一确定的, 192.168.1.32,端口为 503。
Simubox 中的 Aprus(适配器)使用的是 Ethernet(网口)版本,连接到网络交换机,可以用 Modbus TCP 方式与 PLC 进行通讯。
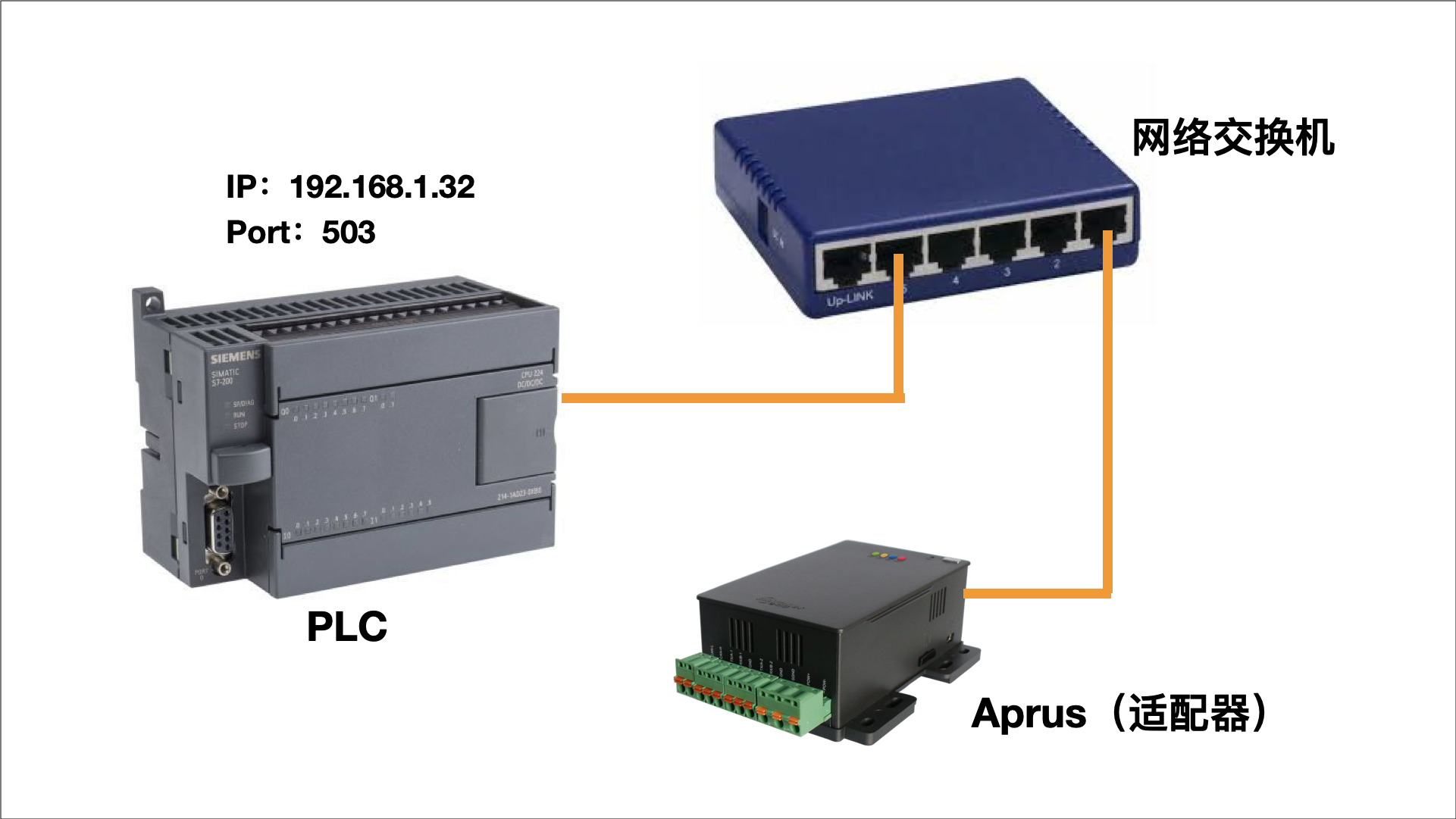
PLC 数据表是确定的,适配器 Aprus 根据这个数据表去采集数据,并向 Mixiot 平台上报数据,上报的格式是按标准的 Mixiot 系统的 R 报文格式:
{ “AprusKey”:”Value”, “AprusKey”:”Value”, “AprusKey”:”Value”, …., “AprusKey”:”Value” }
PLC 数据表及对应的 AprusKey 对照表如下,有了这个表,就可以在 Mixiot 系统中,编写映射表并建立他们之间的映射关系了。
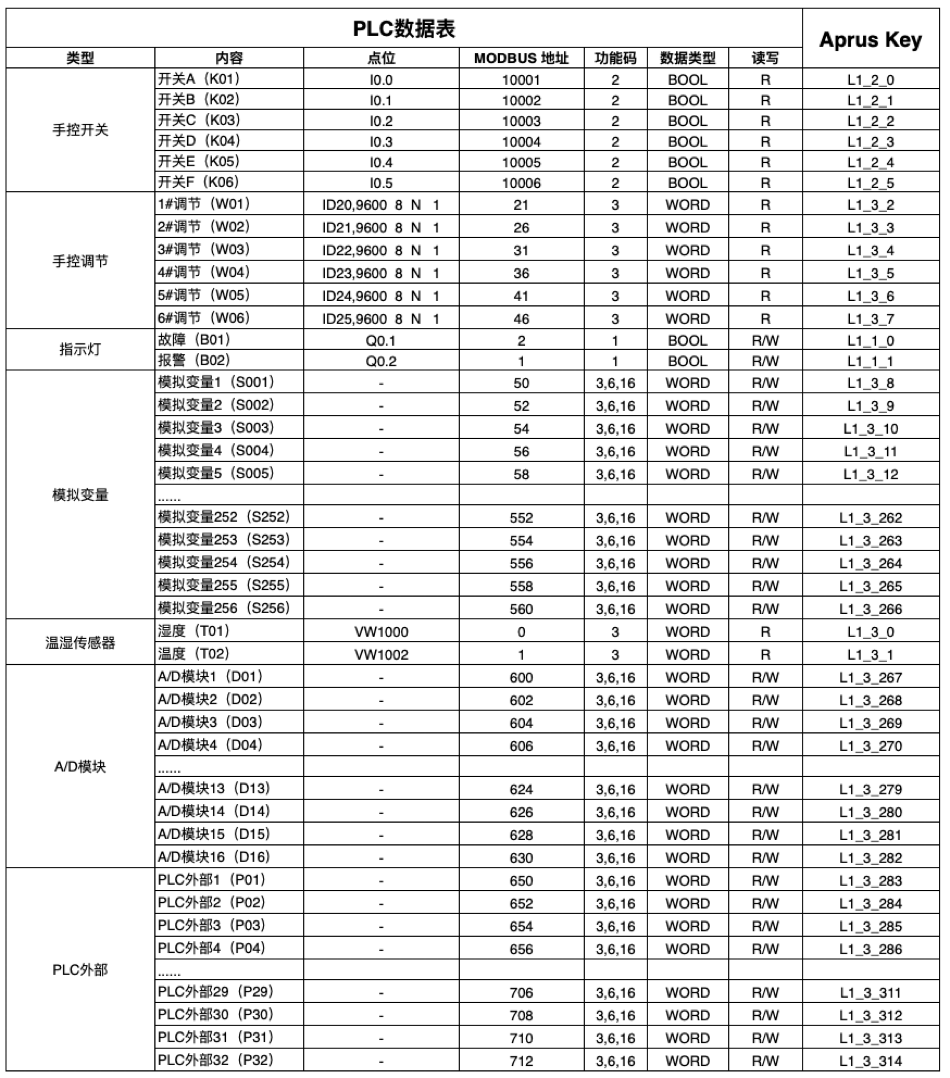
(2)Lua
Simubox 中配有适配器 Aprus,用来采集 PLC 数据。Aprus 中已经烧录了标准的 Lua 程序,包括 aprus.lua 和 config.lua。程序代码如下:
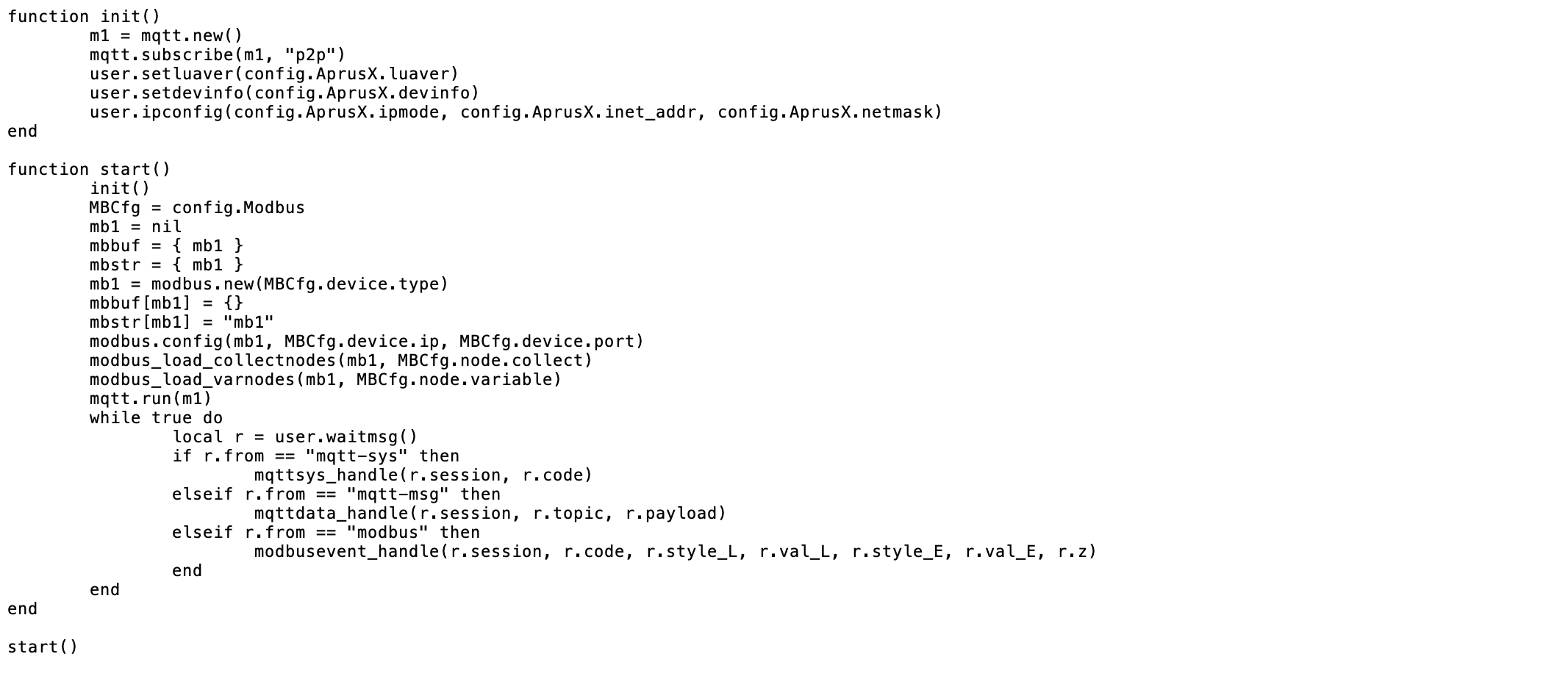
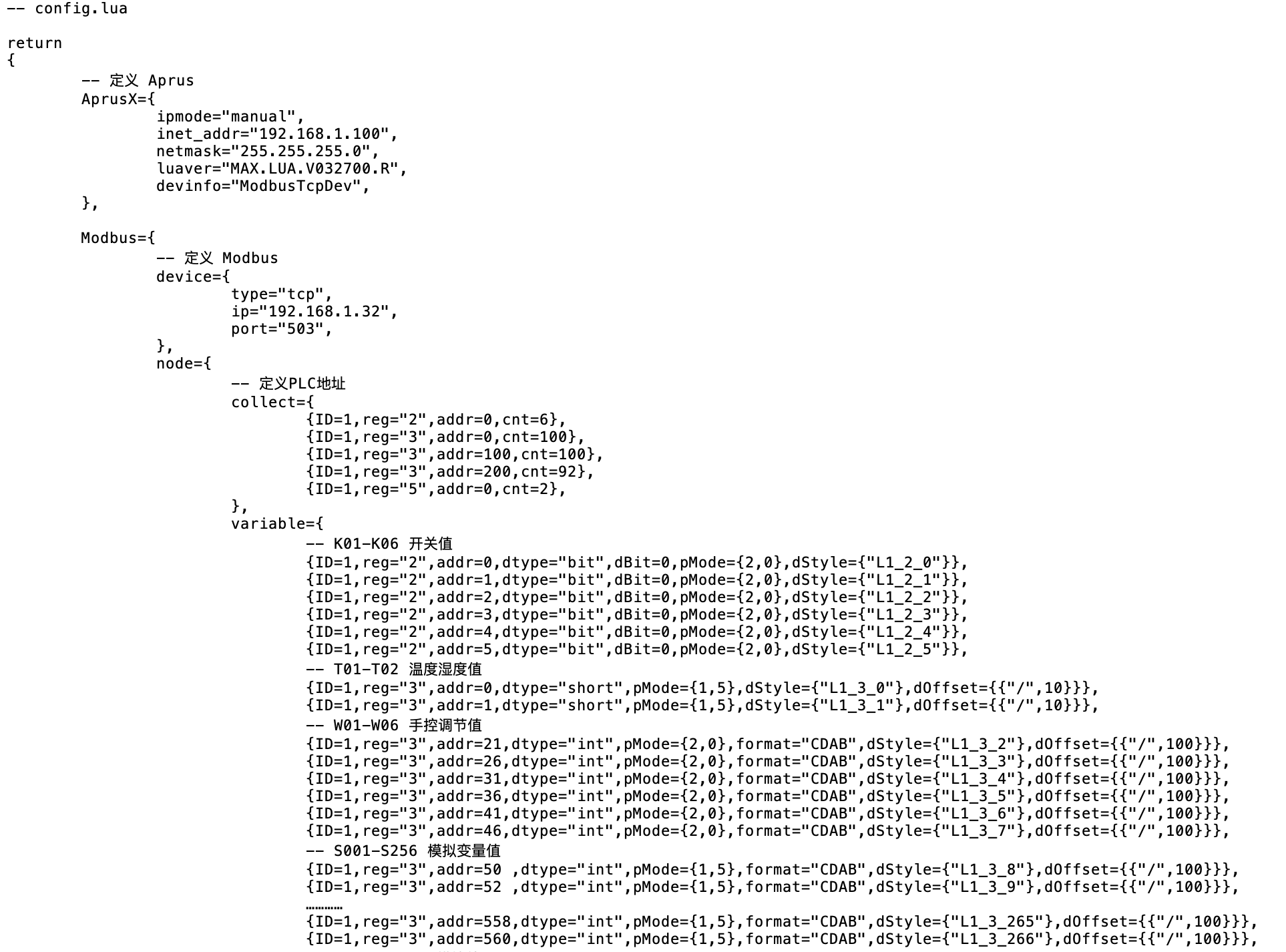
上述程序源代码可以在 http://simubox.mixiot.top 中下载。
