第3节 “指数分析”的使用方法

（一）进入“指数分析”

“指数分析”应用的形式也是标准的MixIOT Indass应用布局：

除了权重计算器外，只有两个菜单板块：分析项目和分析结果，我们根据需要创建不同的指数分析项目。

每一个分析项目，就是需要计算的特定的一种指数。也就是说，我们需要编制一个统计指数，就需要创建对应该统计指数的一个分析项目。

MixIOT 体系应用中，数据分析相关的应用（MixIOT Indass）的几个应用的布局都差不多是这样，除了指数分析，还包括偏态分析、稳定性分析、平衡与增量分析以及风险分析。

按 “+添加” 创建统计指数分析项目：

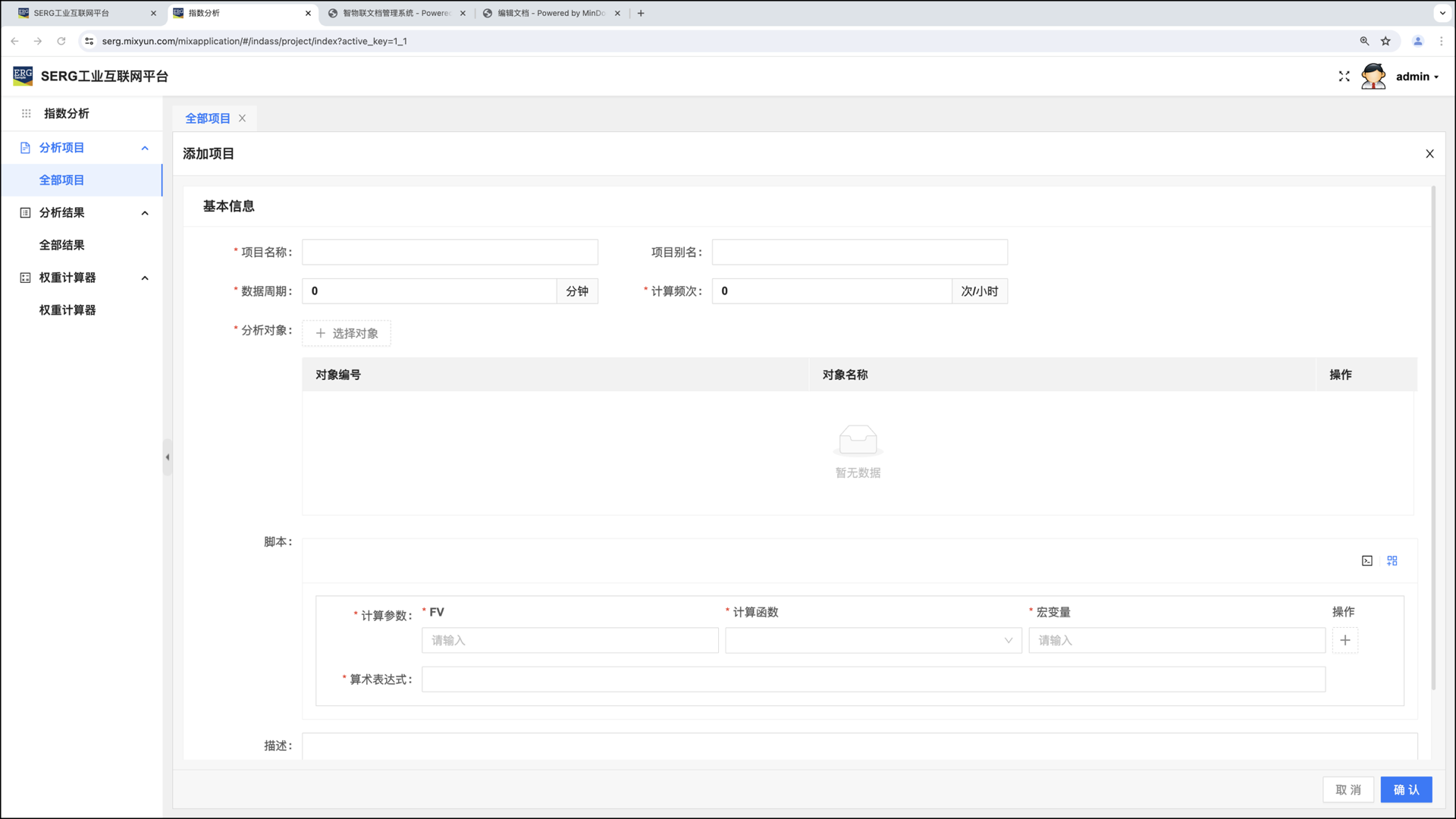
除了项目名称、别名，还有其他的一些项目属性：

（1）数据周期

指统计指数的计算所使用多久以来的数据。一般来说，这需要根据指数编制的要求来确定。通常来说，指数计算的频次无需特别密集，一分钟计算一次，已经是非常高频次了。对一些对象变化不是很大，变化不剧烈的对象而言，可以适当降低计算频次。

（2）计算频次

指多久计算一次。单位是每小时计算多少次，如果每分钟计算一次，就填写60；如果5分钟计算一次，就填写12；如果是半分钟（30秒）计算一次，就填写120。

（3）关联对象

指需要进行该统计指数计算的对象列表。可以通过 “+添加对象” 按钮把需要计算这个指数的对象添加进去。添加对象后，这些对象就会按指数分析项目所规定的频次输出该统计 指数的计算结果。

（4）指数分析脚本

脚本提供纯脚本编辑和界面化方式。

脚本部分有两个内容，一个是对象变量（ FV）的选择以及相关的统计计算方法；另一个是构成统计指数的表达式。

这里需要说明的是，为了书写和使用的简化和方便，在表达式中，我们直接沿用对象变量标识（FV）来代表变量经过统计计算后的结果。

举个例子：

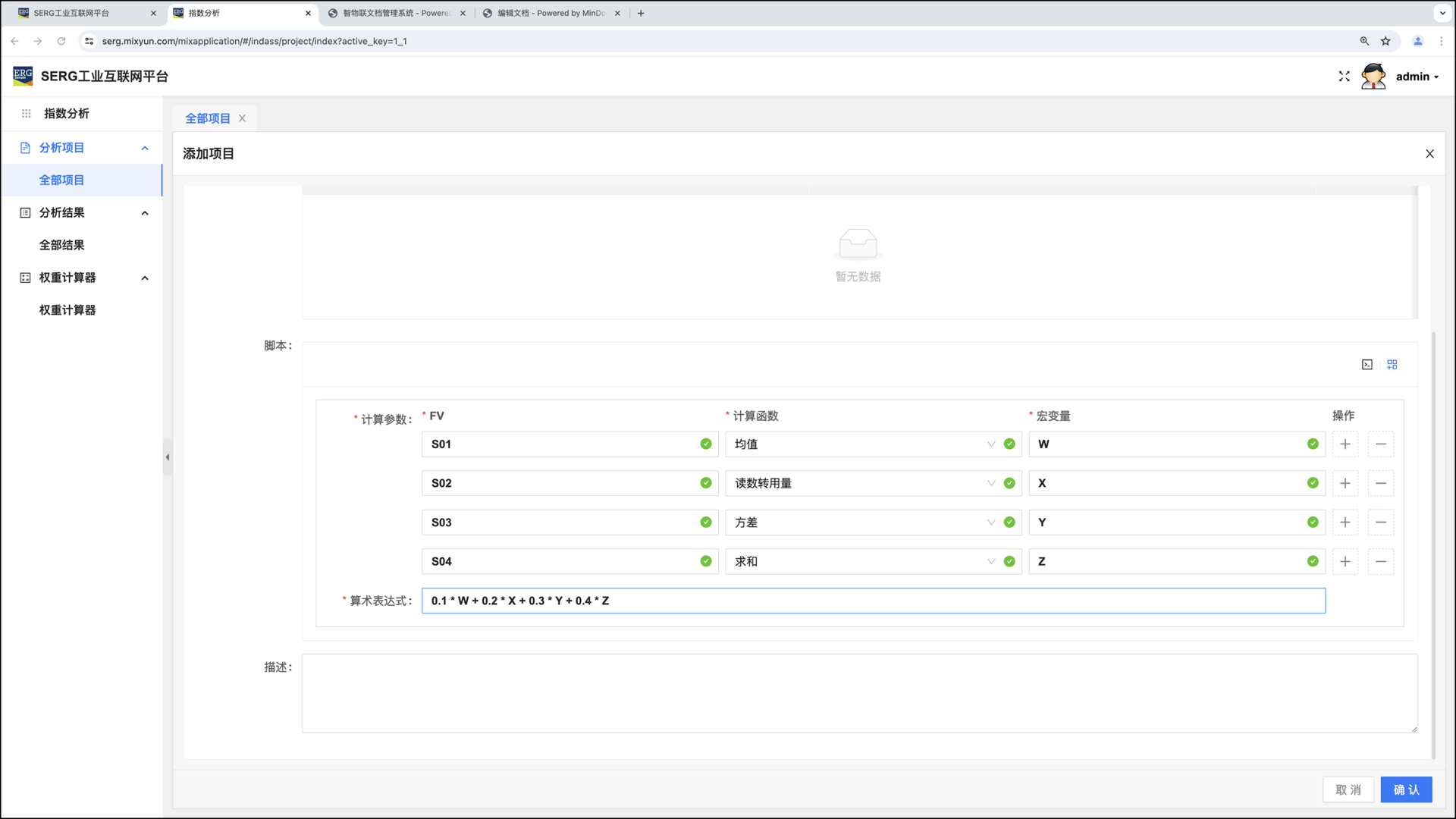
假设 W、X、Y、Z 是4个宏变量，分别代表 FV S01 在计算时段里数据的均值、FV S02 在计算时段里数据的正计数（也就是读数转用量）值，FV S03 在计算时段里数据的方差值，以及 FV S04 在计算时段里数据的总和。

那么，表达式的结果

$Q=0.1W+0.2X+0.3Y+0.4Z$

就是我们要计算的，这个计算时段的指数。

我们可以直接把 “界面” 模式切换成 “脚本” 模式：

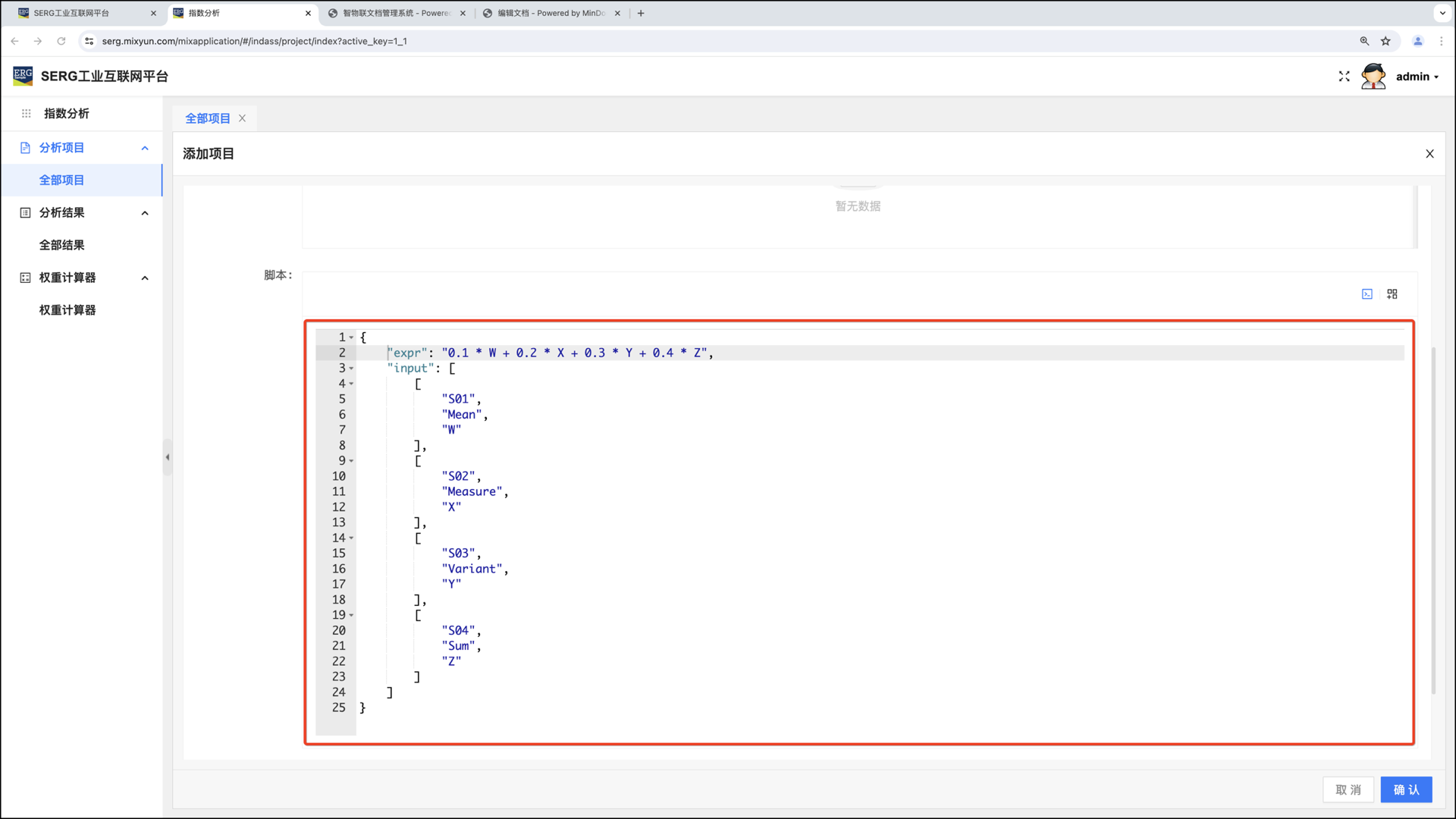
如果是直接在脚本编辑器里面编写脚本，那么这个指数项目的脚本就应该这样写：

{
    "input": [
        [  "S01", "Mean", "W"  ],
        [ "S02", "Measure", "X" ],
        [ "S03", "Variant",  "Y" ],
        [ "S04",  "Sum", "Z" ]
    ],
     "expr": "0.1 * W + 0.2 * X + 0.3 * Y + 0.4 * Z"
}

Mean、Measure、Variant 和 Sum 是分别对应于该对象变量 S01、S02、S03 和 S04 的计算函数。

MixIOT 支持的计算函数可以从界面上看到：

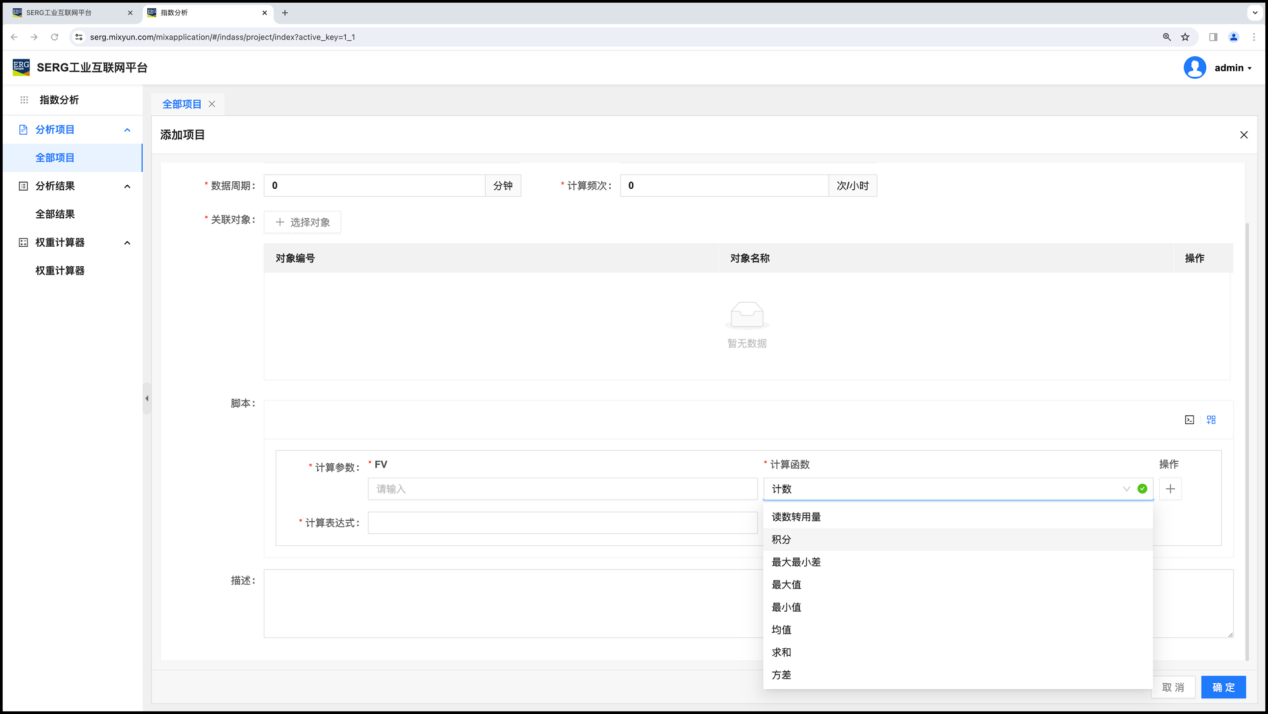
在脚本中对应的写法是：

• Count：计数
• Measure：读数转用量
• Integral：积分
• Margin：最大最小差
• Max：最大值
• Min：最小值
• Mean：均值
• Sum：求和
• Variant：方差

脚本的基本格式是：

{
    "input": [
        [ "对象变量名FV", "计算函数", "宏变量" ],
        [ "对象变量名FV", "计算函数", "宏变量" ],
        [ "对象变量名FV", "计算函数", "宏变量" ],
            ......
        [ "对象变量名FV", "计算函数", "宏变量" ]
    ],
    "expr":  "宏变量的计算表达式"
}

我们在编写表达式时候需要非常小心。指数分析项目中的表达式，只能是宏变量的表达式，如果表达式出现了变量（FV）名，则计算就会出错，整个分析项目不会输出任何计算结果。

所以，我们在创建指数分析项目后，初期需要去检查和验证结果，如果看不到有计算结果输出，那就要回头去检查表达式是不是有错。

（二）创建综合运行指数分析项目

我们将在 “指数分析” 应用中，为三普能源集团旗下的各瓦斯电站创建指数分析项目，但首先要清楚，我们希望要观察什么。

发电机组自身的运行情况，是佳华电站能否正常生产的重要情况，所以第一个指数，我们选择发电机组的 “运行综合指数”，这个指数旨在关注瓦斯发电机组的综合运行情况。

设备运行的综合指数，是一种比较典型和有代表性的指数构造方法。这种统计指数的构造方法相对很容易。我们按如下步骤来构造这个统计指数。

（1）选择一些重要的因素（FV变量）

回顾一下佳华机组的变量情况：

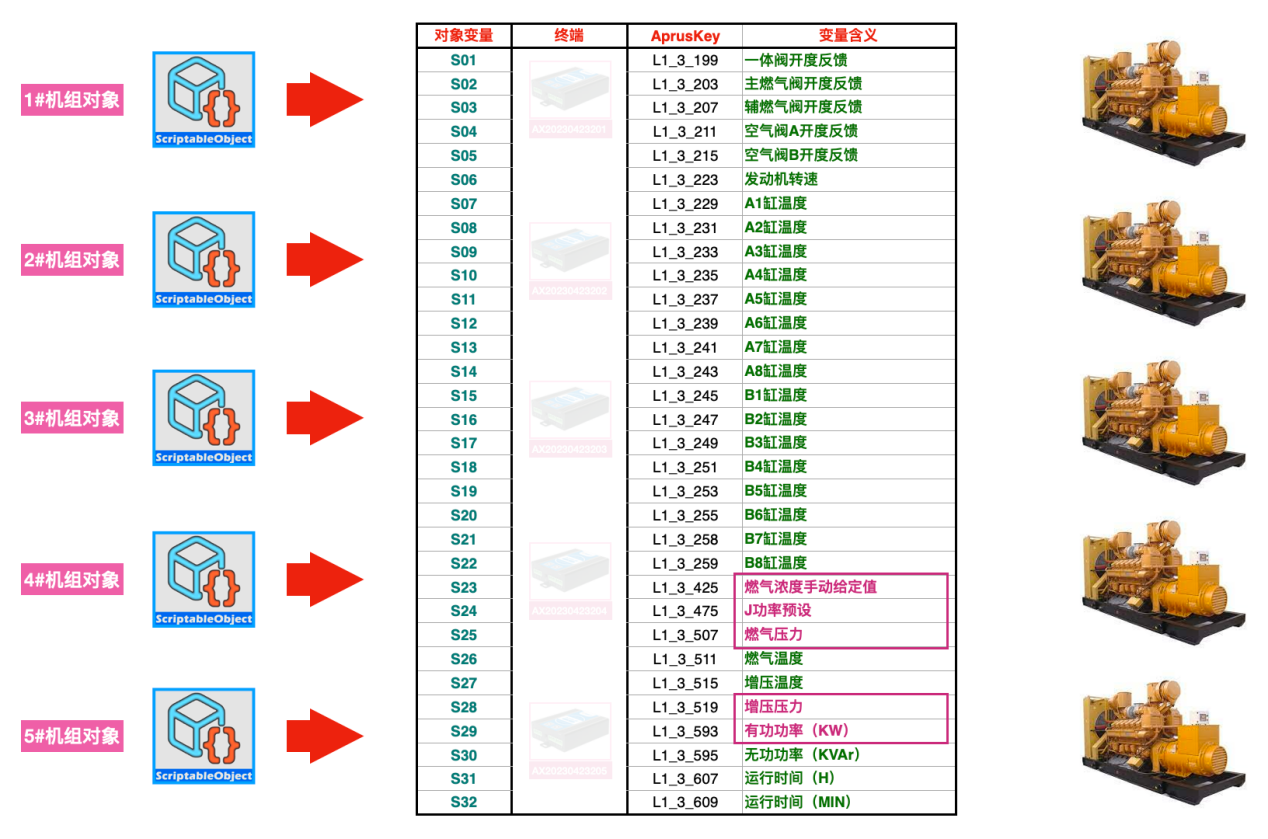
我们可以选择相对比较重要的变量作为统计指数的因素，它们分别是：燃气浓度给定值（S23）、J功率预设值（S24）、燃气压力（S25）、增压压力（S28）和有功功率（S29），这几个指标基本上能反映瓦斯发电机组的运行情况。

要记住，我们构造的是 “综合运行指数”，所以指数因素的选择一定要能够反映 “机组综合运行情况” 才行。

（2）确定权重

上面选择了5个指数因素。虽然这些因素都从不同侧面反映了机组的运行情况，但对机组运行综合状态而言，它们的相对重要性并非完全一样。为了保证综合运行指数能更加完整准确地反映机组的运行情况，就需要确定这些因素的相对重要性比例，这就是权重。

MixIOT Indass 数据分析体系应用中，都配有 “权重计算器”，它可以通过两两因素的相对性，计算出这些因素总体的相对权重。

进入 “指数分析” 应用，打开 “权重计算器”：

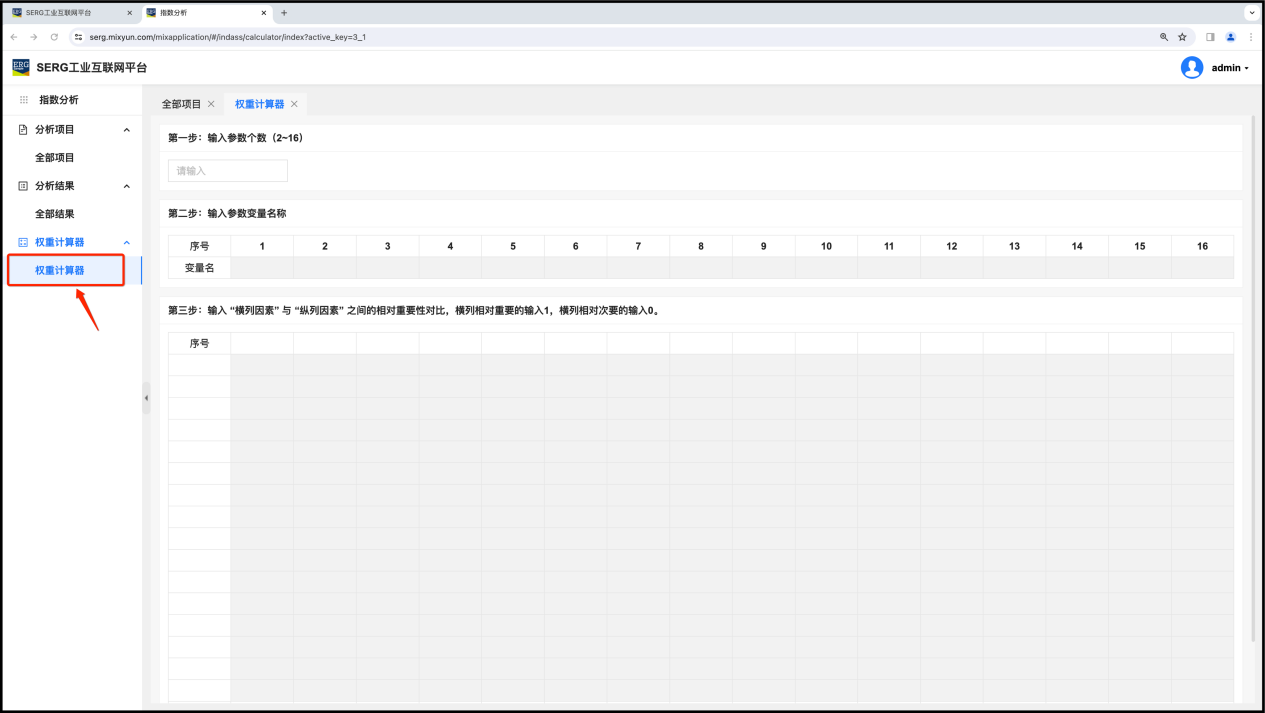
按权重计算器使用步骤提示依次进行操作：

• 先输入参数个数为5；
• 再填写这5个参数变量名，燃气浓度给定值（S23）、J功率预设值（S24）、燃气压力（S25）、增压压力（S28）和有功功率（S29）；
• 最后，按“横-纵”因素的两两重要性比对：相对重要（或相同重要）的输入1相对次要的输入0。

如下图所示：

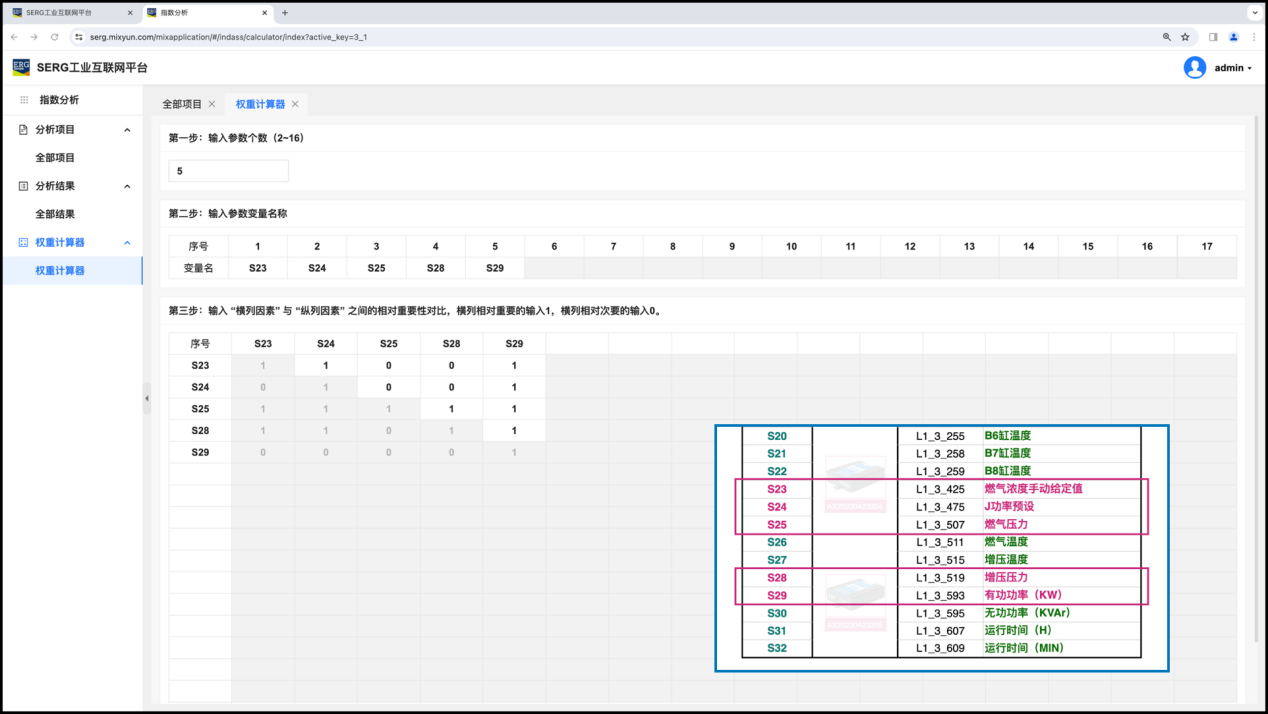
然后，点击 “提交”，获得计算结果：

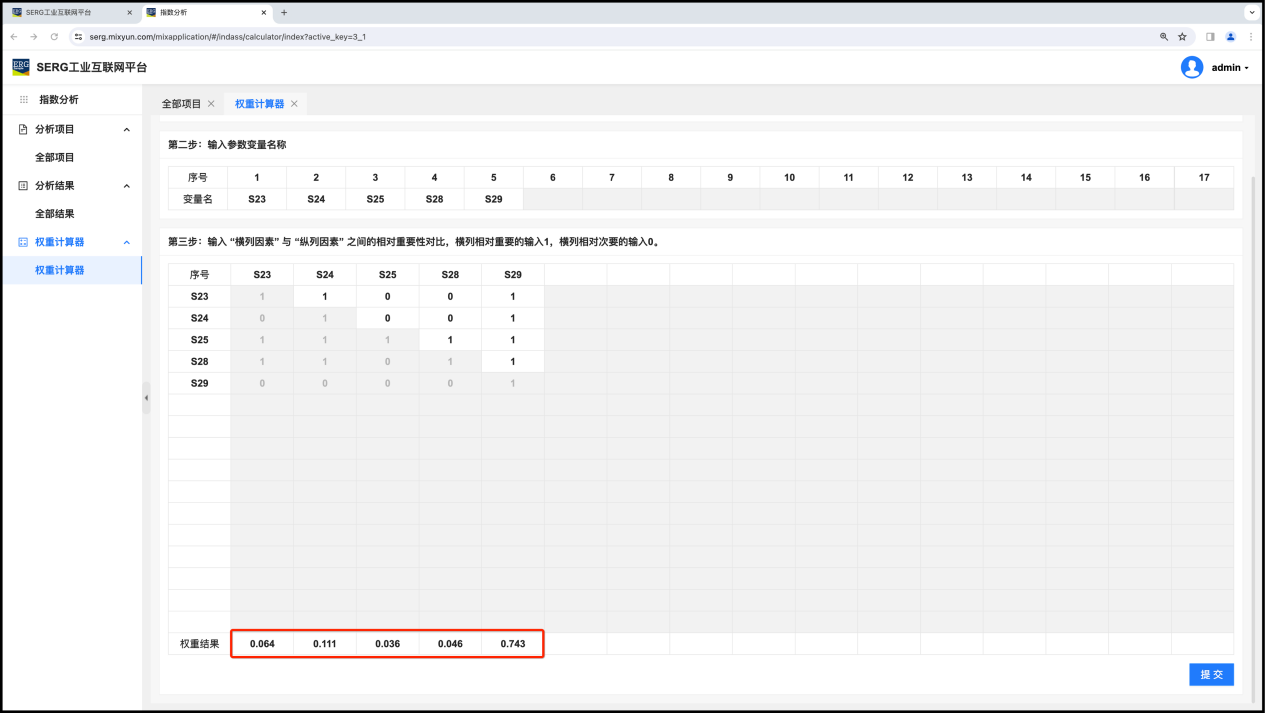
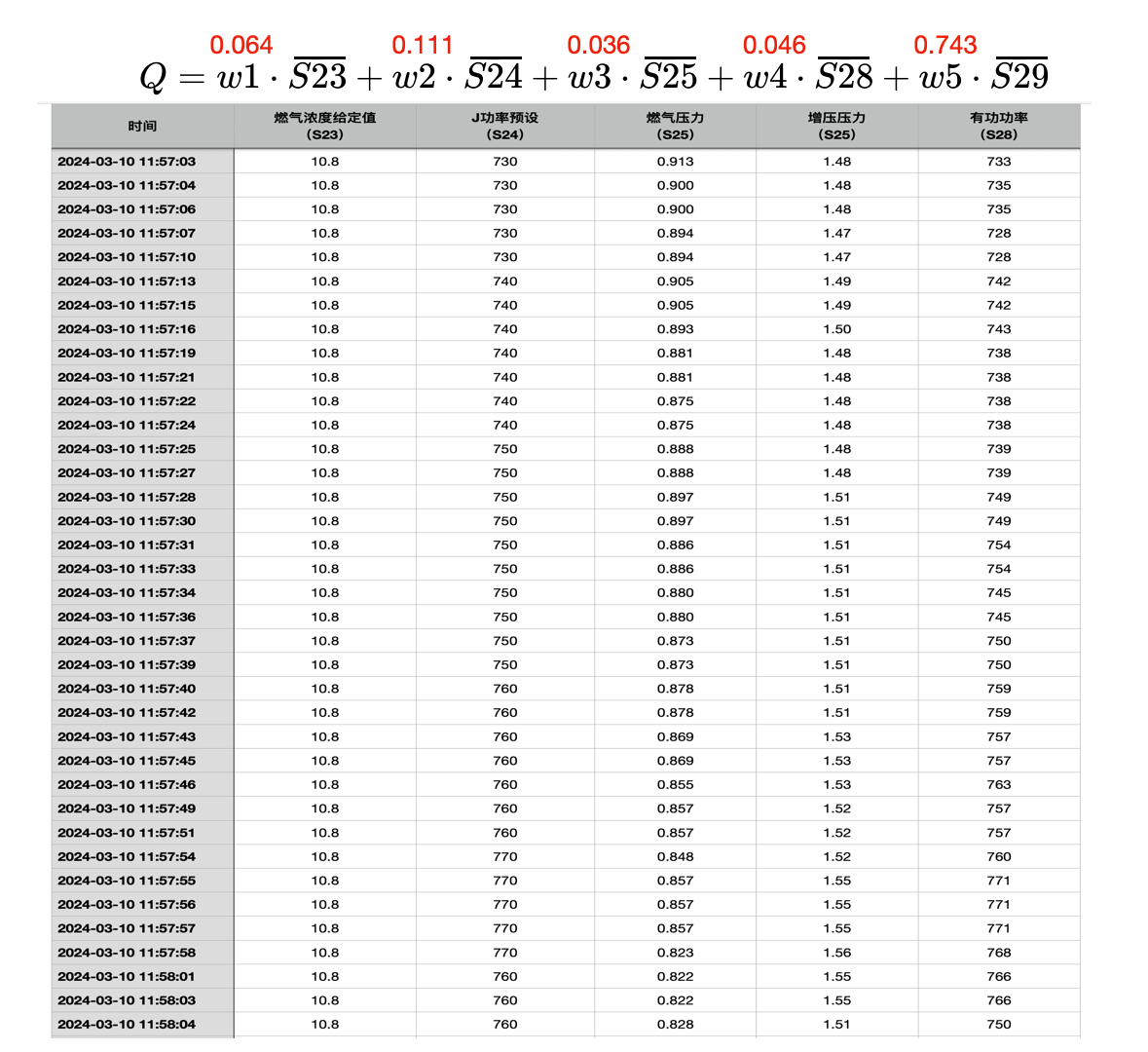
也就是说，S23（燃气浓度给定值）、S24（J功率设定）、S25（燃气压力）、S28（增压压力）和S29 （有功功率）因素的权重分别是： 0.064、0.111、0.036、0.046和0.743。

（3）指数构造

有了统计指数因素（变量）以及这些因素的权重，我们选择简单的构造方法：

$Q=\omega_1* \bar{S23} + \omega_2 * \bar{S24} + \omega_3 * \bar{S25} + \omega_4 * \bar{S28} + \omega_5 * \bar{S29}$

其中， $\omega_1$ ～ $\omega_5$ 就是各自因素的权重值，分别是：0.064、0.111、0.036、0.046和0.743；

而 $\bar{S23}$、$\bar{S24}$、$\bar{S25}$、$\bar{S28}$、$\bar{S28}$、是对象变量 $S23$、$S24$、$S25$、$S28$和$S29$ 在计算周期内的平均值。

（4）创建统计指数分析项目

进入“分析项目”菜单板块，按“+添加”分析项目 ：

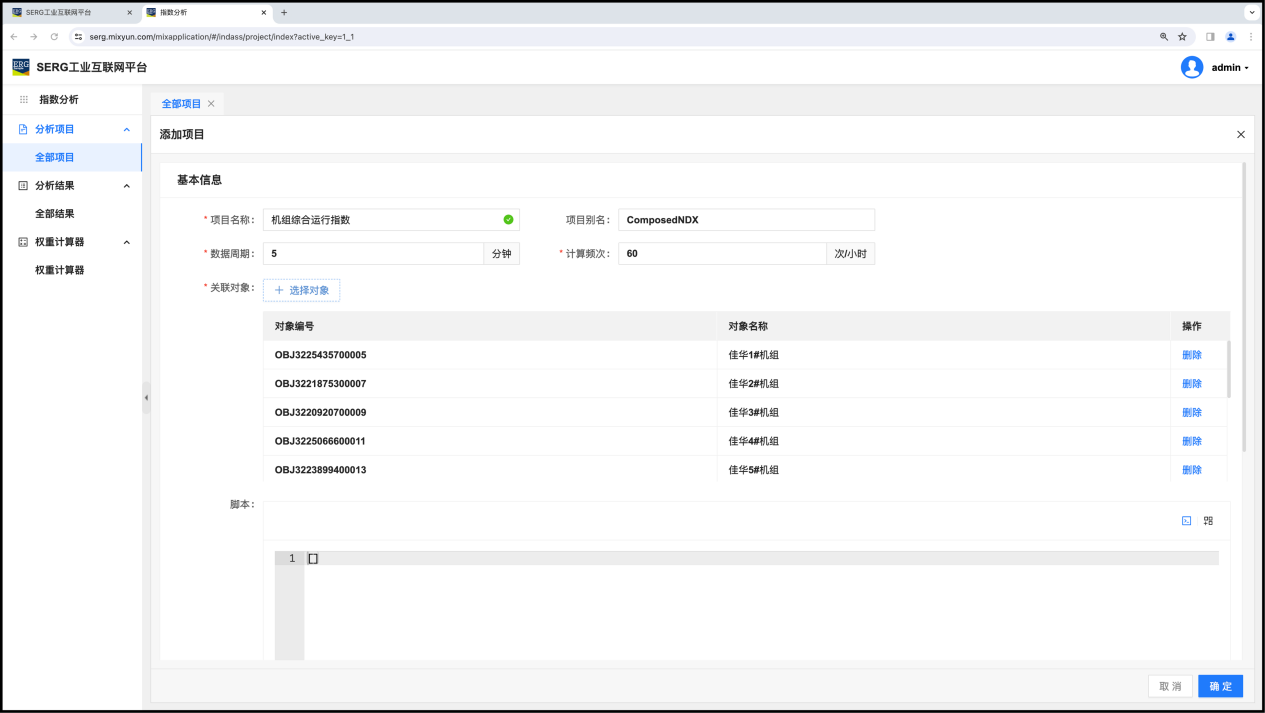
• 项目名称为 “机组综合运行指数”，别名为 “ComposedNDX”。
• 数据周期为5分钟，意思是，每次计算所用个的数据，最近5分钟的数据。
• 计算频次为60（次/小时），每小时计算 60次，也就是每分钟一次。
• 关联对象，可以选择全部单台机组对象。

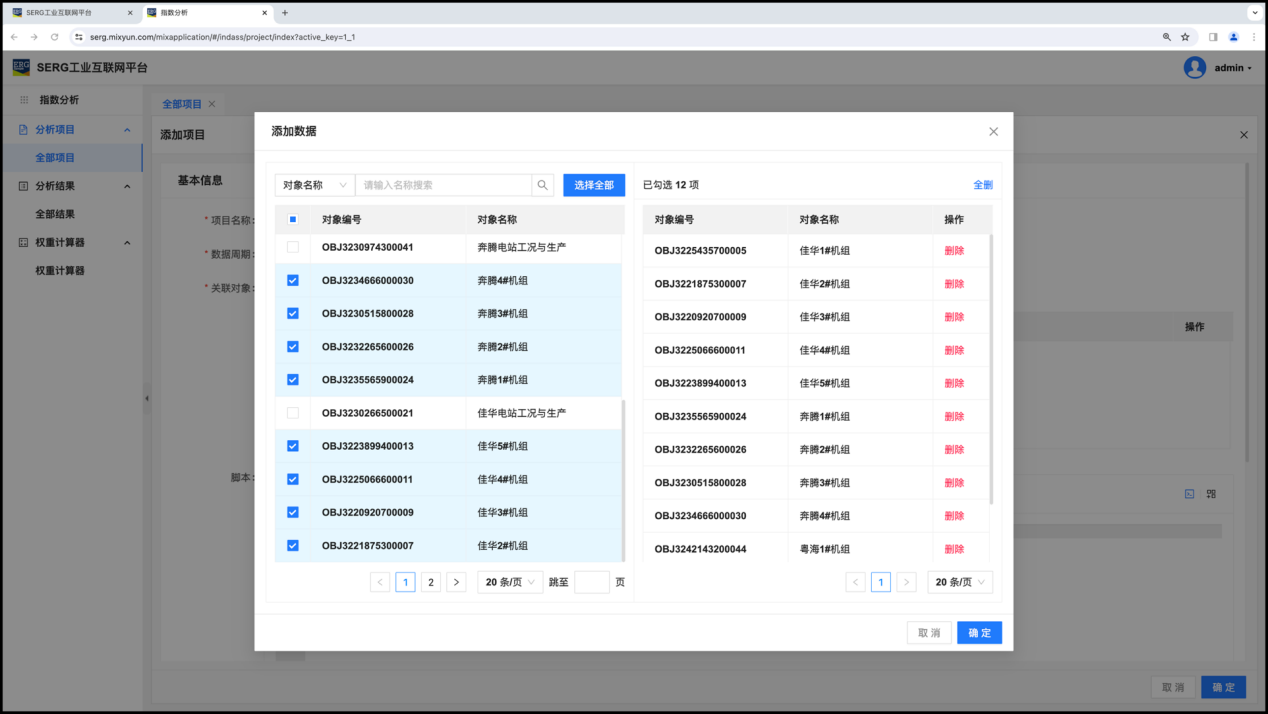
只要对象的变量（FV）命名相同，就可以选择。

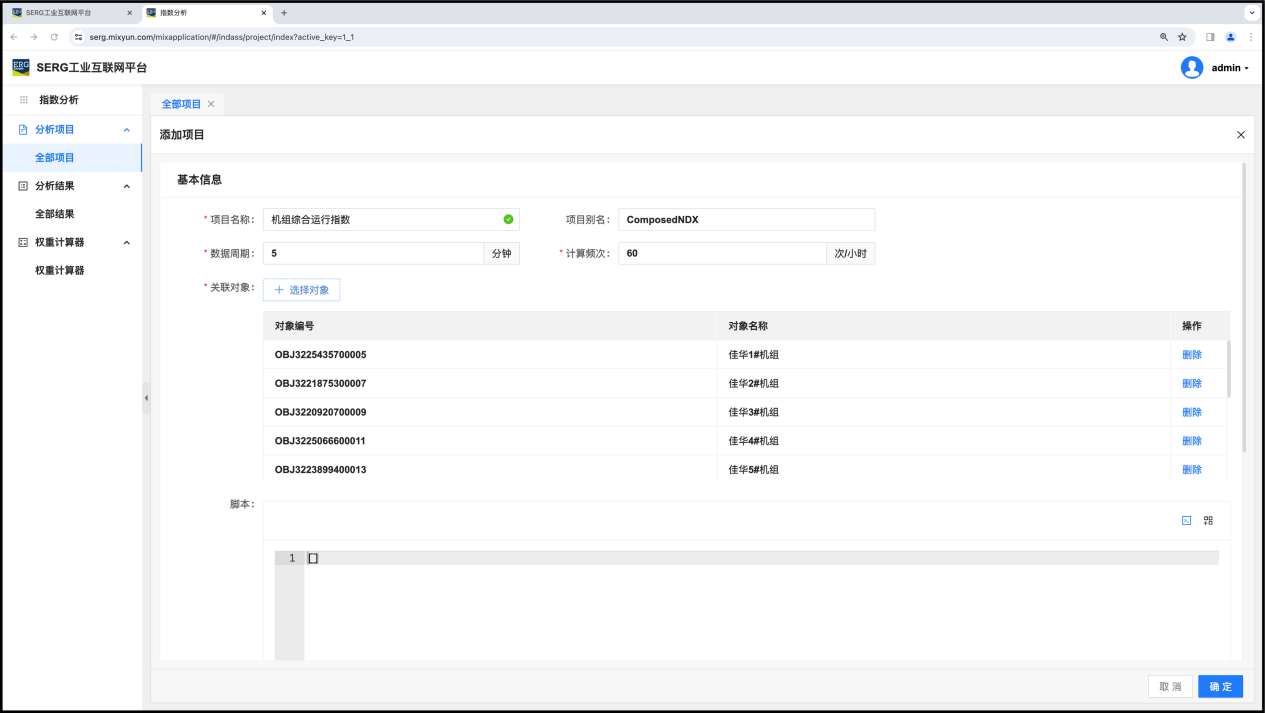
这样，这个项目每分钟输出一次所有机组综合运行指数的计算结果。每个计算结果所使用的数据，都是？？？？？

（5）完成项目脚本

跟其他的应用一样，“指数分析” 应用的核心部分也是指数计算脚本。有了变量，有了变量的权重，有了计算公式，我们就可以编写脚本：

如果不喜欢写脚本，也可以用界面化的方法来完成脚本：

做完了这些，就可以确定保存这个指数分析项目 ：

项目创建完成后，就可以在操作菜单里面 “启动” 运行这个指数分析项目。这个指数分析项目启动后，每分钟会输出一次每台机组的综合运行指数。

（三）综合运行指数的物理意义

我们以一个时间段的机组数据为例来说明 “综合运行指数” 的意义。

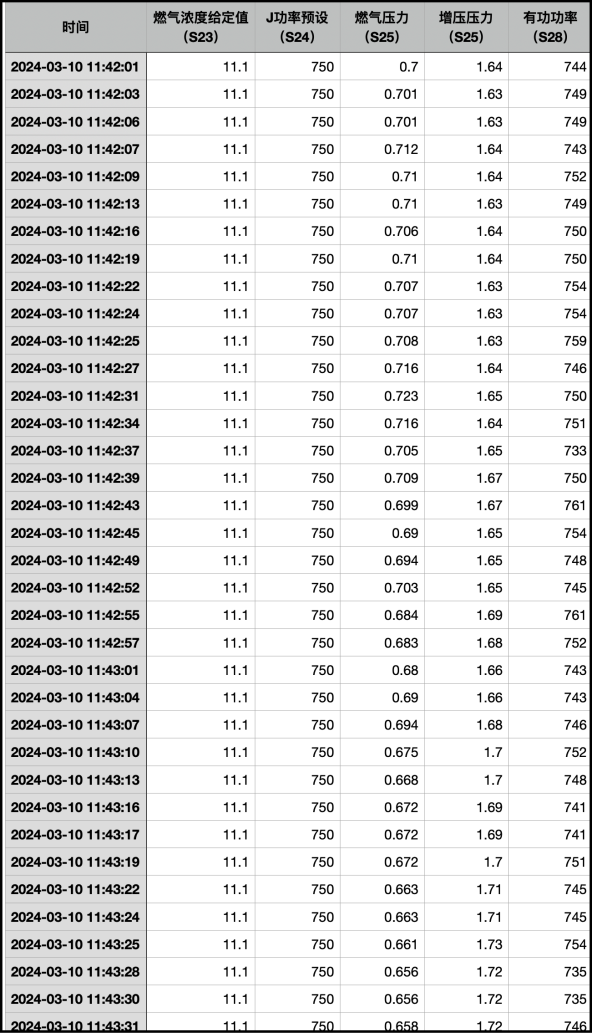
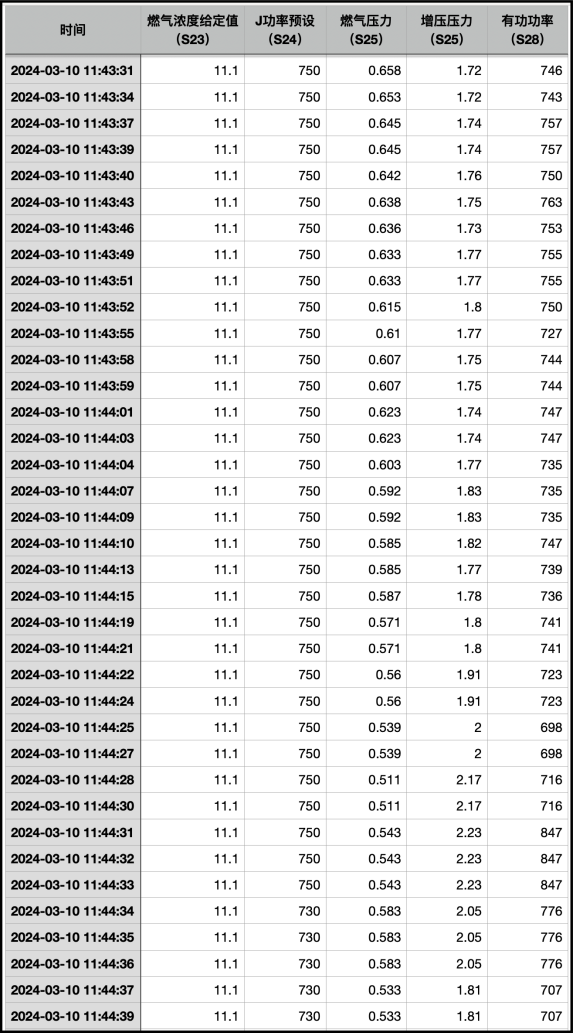
拆解一下指数和权重：

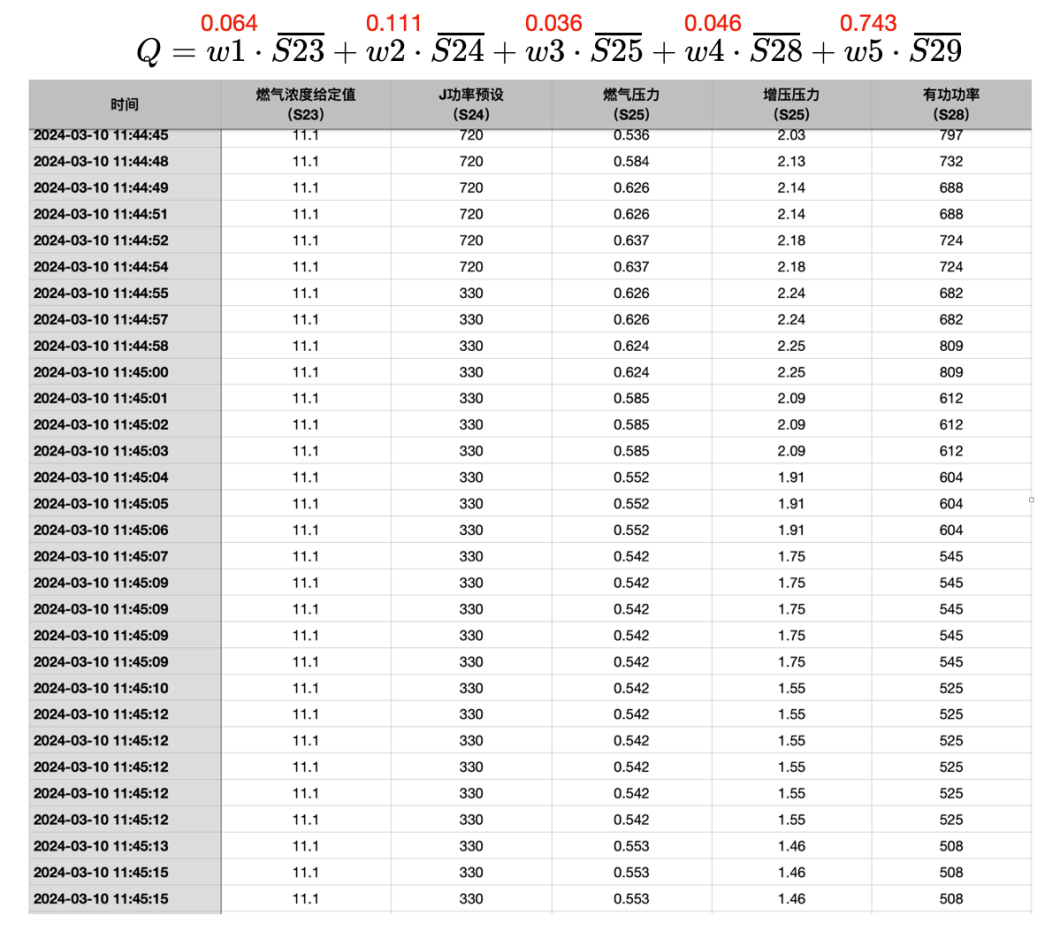
我们挑选一个数据变化比较大的时段。看到这些数据，基本上对这个指数的水平（值）和变化可以有一个大概的估计。一个是指数所选的因素（变量）数据值的大小，另一个是对应于这个因素（变量）的权重大小，这样就对这个指数是怎么回事基本上就心里有数。我们的目的是想知道，哪些因素的变化，会影响这个指数的变化；不仅如此，还希望能知道，指数的变化代表可能所构造的这个指数的哪个因素的变化，以及变化程度、变化速度。

比如，在这个指数构造中，S25 （燃气压力）值本身很小，计算周期的均值也很小，而且S25对应的权重是最小的，只有0.036，那它们的乘积就更小。也就是说，燃气压力的变化，基本上对指数Q的结果基本上没有什么影响；反之，我们从指数Q的变化中，也观察不到燃气压力的变化。

我们看一下计算出来的指数的情况，这是一个360分钟（6小时）的指数变化图：

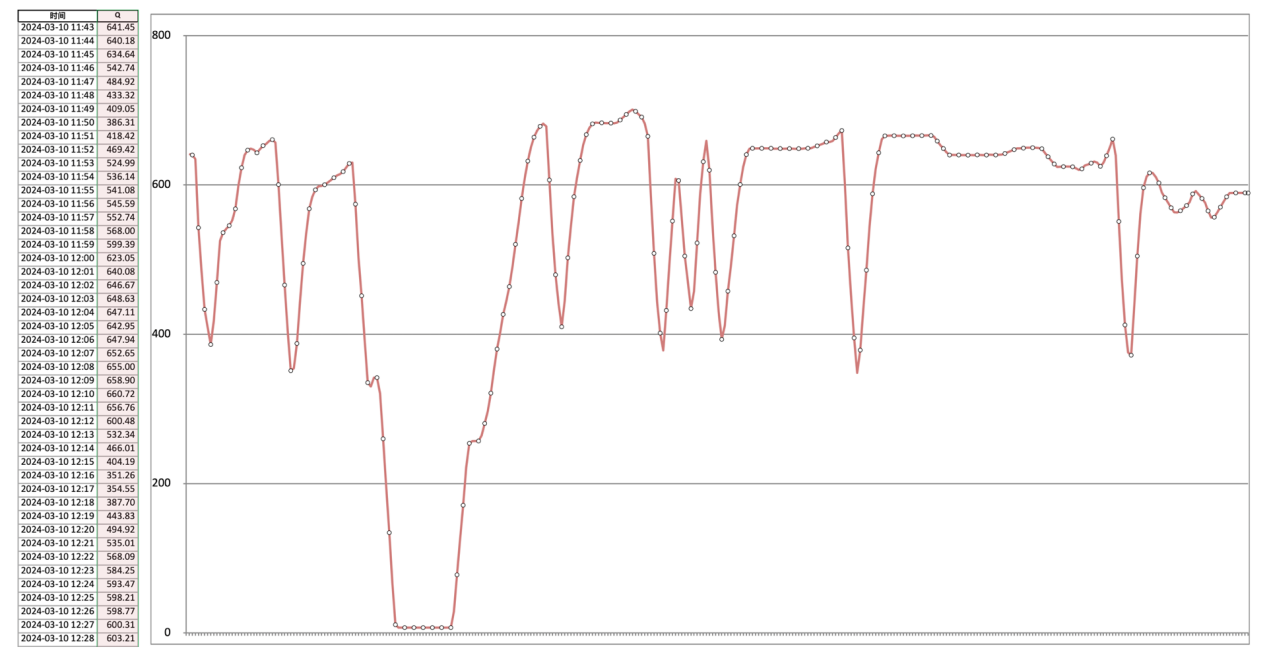
放大一个20分钟的指数变化图：

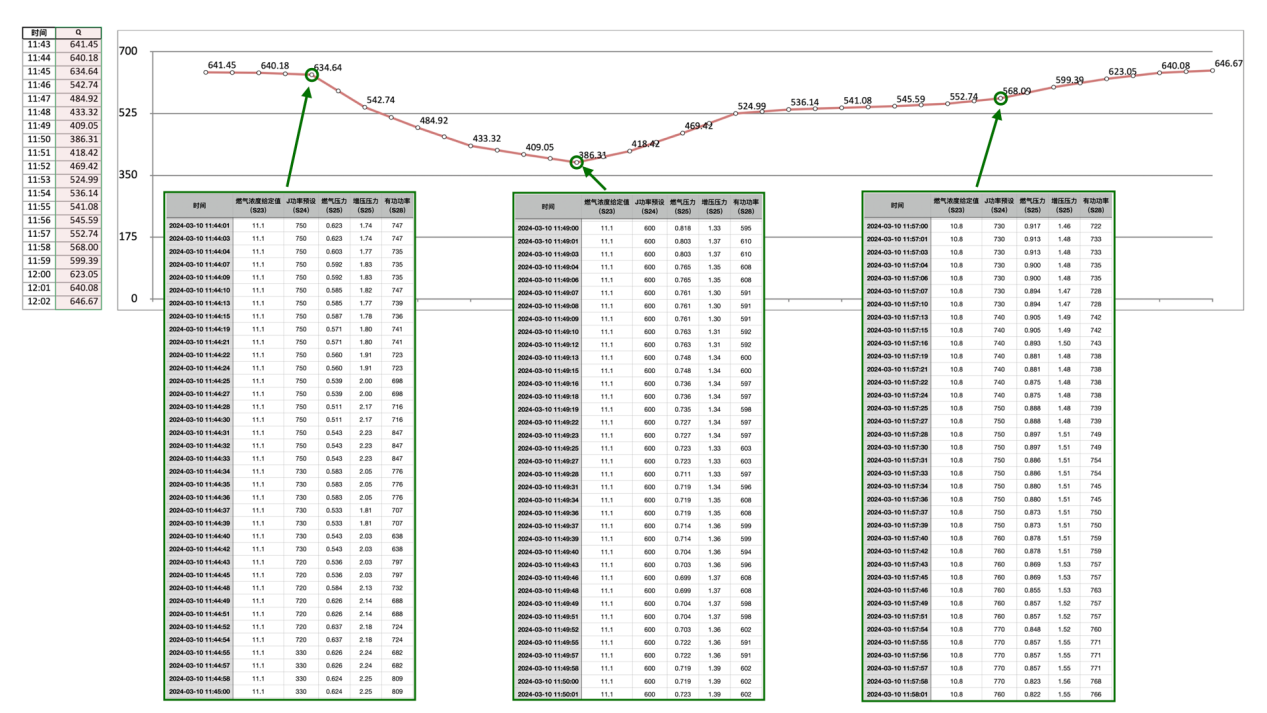
如果对照构成指数的5个参数的数据，其实就很容易发现，综合运行指数Q与实际数据是怎样的一个对应关系。

这个指数的计算频次是每分钟一次，但每次计算的数据是最近的5分钟数据，换句话说，每分钟所计算出来的指数，其中有4分钟的数据是重复的，我们称为 Overlaped Index。这样做的目的，就是为了让指数的变化相对平滑，不至于大起大落，便于进行指数分析。

（四）因素等效比例

前面一种指数的构造中，所选择的因素（变量）、权重分配以及指数公式本身并没有什么问题。但是一旦结合实际数据，好像就出现了问题：

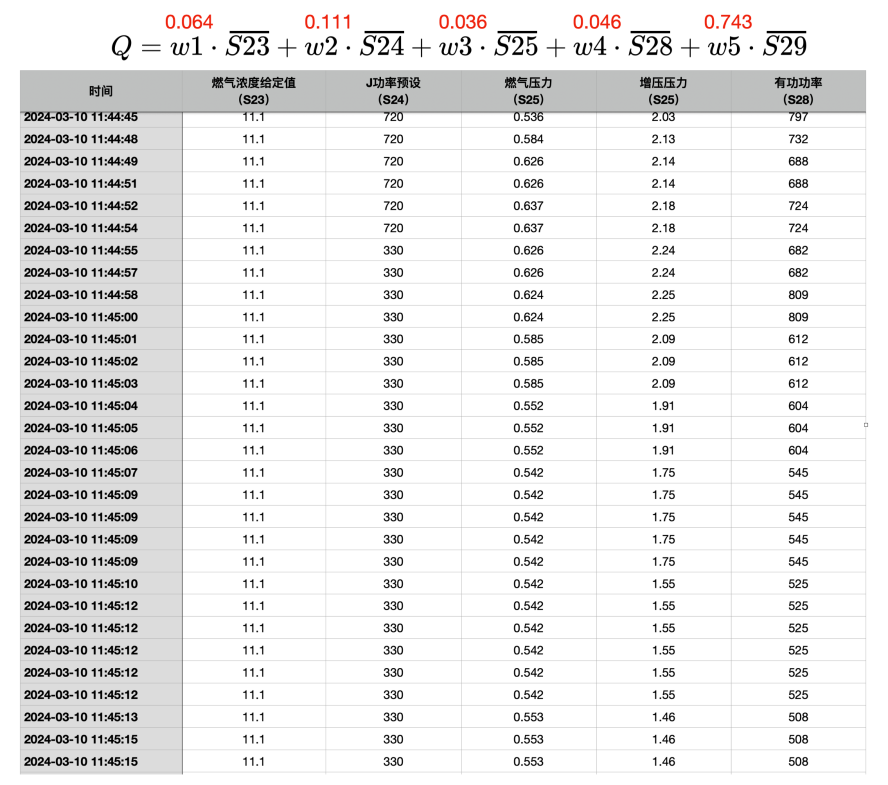
比如 S25（燃气压力）、S28（增压压力）以及S23（燃气浓度给定值）这几个因素权重很小，而且数据本身也很小。

如果因素的数值（变量值）很小，而且这些变量的权重也很小，如上面的S25（燃气压力），数值都是零点几，而权重只有百分之三点几，那么，这个因素对这个指数来说，事实上算是可有可无。

如果遇到的是另一种情况：

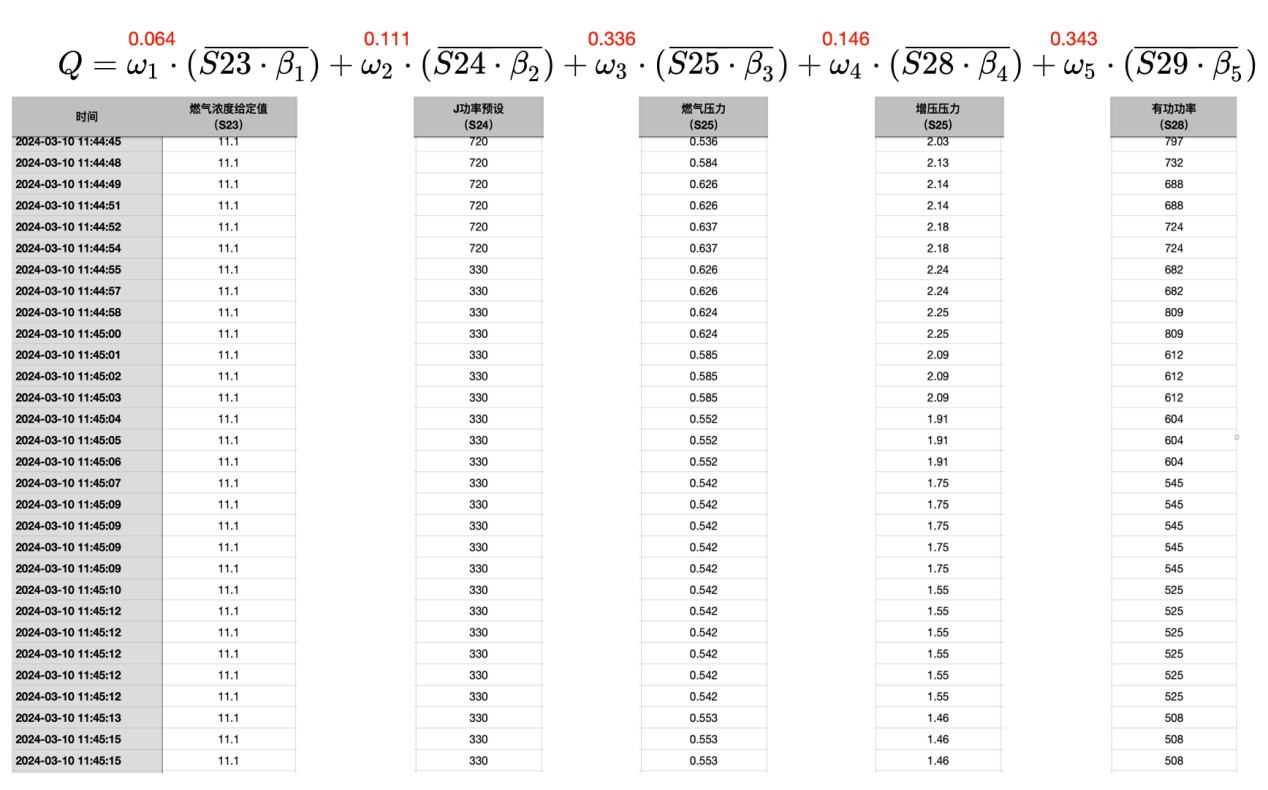
还是以S25（燃气压力）这个因素为例。如果这个因素的权重是0.336（33.6%，三分之一强），说明这个因素很重要，而这个变量的值却很小。这个时候，可以对这个变量的数据进行倍数级的放大。也就是说，让这些权重大的因素的值，不要区别太大。这样做的目的，就是让某个因素发生变化的时候，对综合运行指数Q具有一定的影响力，也就是说，这些因素变化会导致综合运行指数Q的变化。

比如上面的这个情况，我们可以设定β3 = 100 ，这样可以看到，S25 的数值范围大概就是五六十（或七八十），这个数值的变化会导致综合运行指数Q发生变化，这种指数的构造方法，也是常见的方法。这里针对特定因素（变量）的β,就是对应该因素的等效比例（或者等效倍数）。

（五）综合变化指数

前面的指数是综合运行指数，指数水平和指数变换跟构成指数的各因素（变量）的值的大小有直接关系。这种指数水平反映的更多的是指数对象的状态水平。

还有一种综合运行指数的的构造方法，如下面公式所示：

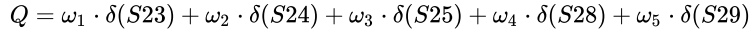
其中：

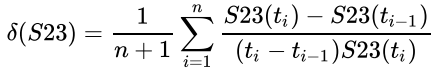
δ(S23)的意思是因素S23的平均变化比率，可以用一个几何图示来说明，δ(S23) 是什么含义。

假设在指数计算时段内，因素 X 有 n+1 个时刻的数据点，分别是 X(tj)，j=0～n。

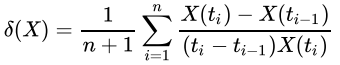
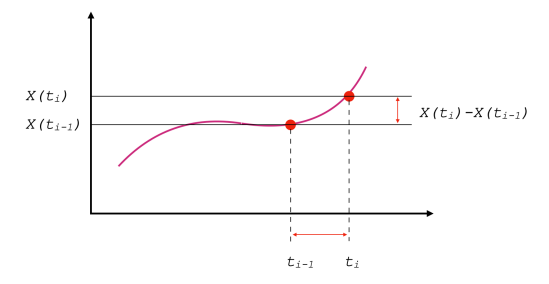
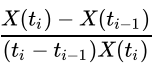
的意思是因素 X 从时刻 ti- 1 到 ti 的时候，单位时间因素变化比例，这样我们就容易理解，δ(X) 的意思是这些变化的平均比率。这种平均变化比率，从整体上反映了对象的综合变化情况。指数的值越高，说明对象的总体变化程度就越大。

我们也可以通过这个变化指数的变化速度，来估计对象变化的速度。只要把δ(X)做一些变形就很容易看到：

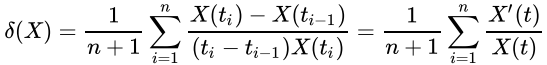
那么，

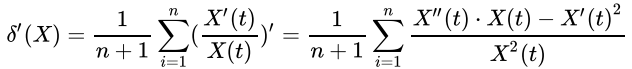
我们用 Q 表示变化程度：

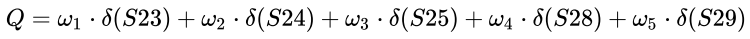
那么，变化速度 VQ：

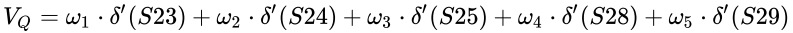
对一个对象而言，可以通过对综合运行指数和综合变化指数这两个指数的观察，得到对象状态总体程度和变化程度的量化。还可以通过对综合变化指数的数值微分计算，知道对象变化速度。

对一个复杂的对象而言，这些都是非常重要的指标。

（六）指数因素的相关性

构造指数的因素在选择的时候，一般需要避免选择具有强相关性的因素。在上面的两个指数构造中所选择的因素中：

其中，因素 S24（J功率预设）和因素S29（有功功率）之间是一个强正相关的关系。整个机组运行的时候，有功功率的（S28）实际上是围绕 S24（J功率预设）变动的，基本上呈正态分布，也就是说，基本上满足 μ(S29)=S24。

一般来说，我们可以只选择这两个因素之一作为指数因素（变量），比如可以只选择S29（有功功率）作为指数因素。如果必须同时要选择两个相关性强的因素，那么，其中一个指数因素的权重就不能很大，通常不应超过另一因素权重的15%。

（七）指数因素的权重

构成指数的因素对指数很重要，指数因素的权重对所构造指数也非常重要。简单地说，指数因素的权重，就是对应因素的重要性比例如何量化和分配。
MixIOT 的权重计算器，使用了赛亚特标度（AHP标度）对因素做两两重要性的比对，这个方法会使得权重的分配更加精准合理。

赛亚特标度（AHP标度）用于两两比较决策元素，其值范围从 1到9，具体含义如下：

1：表示两个元素同等重要；
2：表示两个元素之间的重要性比较接近，但仍有细微差别；
3：表示一个元素比另一个元素稍微重要；
4：表示两个元素之间存在明显的重要性差距，但不是极端；
5：表示一个元素明显比另一个元素更重要；
6：表示一个元素的重要性明显高于另一个元素，并且这种差别非常明显；
7：表示一个元素比另一个元素强烈地更为重要；
8：表示两个元素之间的重要性差距非常显著，接近极端；
9：表示一个元素相对另一个元素极为重要。

对于介于这些基本评分之间的判断，还可以使用上述整数值之间的中间值（如1.5、2.5等）来表示它们的评估。使用赛亚特标度的目的和好处可以归纳为：

• 量化主观判断：赛亚特标度允许将主观判断转化为可以比较和计算的量化值。
• 提高决策一致性：通过一致性比率的检验，可以评估决策矩阵的一致性，检查和改进它们的判断，确保判断过程的合理性和一致性。
• 适用于复杂判断：对于包含多个标准和选项的复杂决策问题，赛亚特标度提供了一种有效的工具，系统地比较和评估不同的因素的重要性。

MixIOT 的权重计算器，会对所选择的比对值做出客观的合理性和一致性计算。这是因为在进行两两元素重要性比对的时候，很容易出现自相矛盾的地方。

比如，“A比B重要， B比C重要，C比D重要，但D又比A和B都重要”。这就很显然出现了自相矛盾的地方，而一致性的验证，就是对一致性进行量化。

画一个图来解释这个过程：

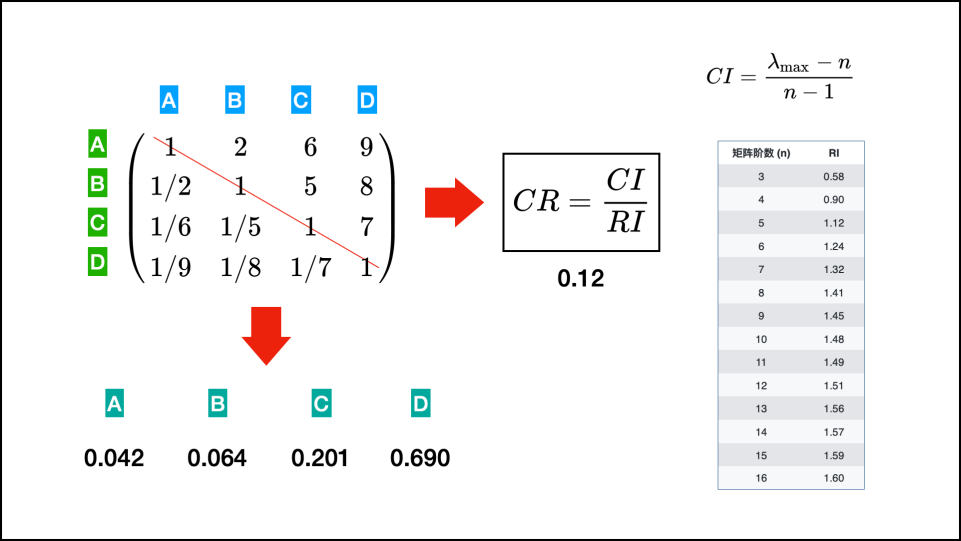
假设现在有4个因素（A、B、C、D），我们以横列的因素与纵列的因素两两比对，比对的结果是这样的：

• 对角线是本因素自己跟自己比对， 比对结果当然是1，因为重要性一样；
• B与A的比对是2，所以反过来，A与B的比对是1/2；
• C与A的比对是6，也就是说，A与C的比对是1/6；
• D与A的比对是9，这样，A与D的比对就是1/9；
• C与B的比对是6，B与D的比对自然就是1/6；
• D与C的比对是7，也就是C与D的比对是1/7；
• D与 B的比对是8，这样B与D的比对是1/8。

比对完成后，权重的决策矩阵也就出来了。不难看到，决策矩阵的对角线元素都是1，而决策矩阵的对称位置的元素都是互为倒数。

这个权重决策矩阵的权重计算结果为，wA=0.042、wB=0.064、wC=0.201、wD=0.690。但这个结果是否合理准确，就需要计算一致性比率CR。

一致性比率 CR是一致性指数（CI）与随机一致性（RI）之比，如果一致性比率算出来 CR < 0.1，说明这个决策矩阵的合理性和一致性没有什么问题；

如果一致性比率CR=0.1，说明一致性有问题。这里计算的结果是0.12，虽说差距不大，但还是说明这个一致性是稍有问题，需要进行调整。