我们用 MixIOT 对象的 n个变量(权重因素)来考察该对象的稳定性,这些变量在某个时间段里面时序数据可以表示为:
X(t) = {X1(t),X2(t),X3(t),……,Xn (t)} t = t0,t1,t2,t3,……,tm
每个因素对应的权重是:w1,w2,w3,……,wn。
我们用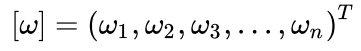
来表示。其中 Xi(t) 是 MixIOT 对象变量 Xi 在 t 时刻的值,t0~tm 是某个时段 [T] 的所有时刻。
如果我们把 MixIOT 对象在这个时间段的所有时序数据放到一起,如果把他们当做一个矩阵 [X], 那么这个矩阵 [X] 就是这个样子:
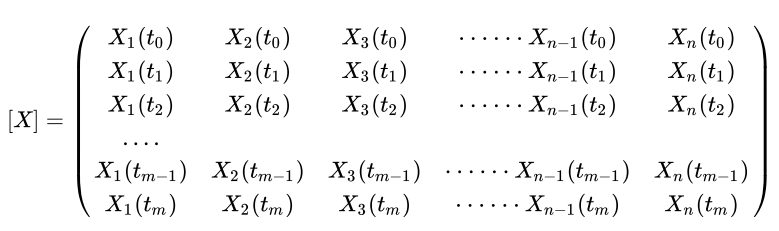
那么,这个 MixIOT 对象的稳定性,实际上就是上面这个矩阵 [X] 和 [ω] 稳定性函数 S:
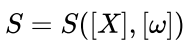
这是一个多因素(变量)的稳定性问题,所以,它本身就是比较复杂的问题。
为了搞清这个复杂的问题,先要了解单一因素的稳定性是什么。现在来看某个单一因素(变量)Xi(t) 的稳定性是什么。
我们把变量 Xi(t) 在 [T] 时段所有时刻的数据可以这样来表示:
Xi(t) = {Xi(t0),Xi(t1),Xi(t2),Xi(t3),……,Xi(tm-1),Xi(tm)}
这是一个单因素的时间序列。
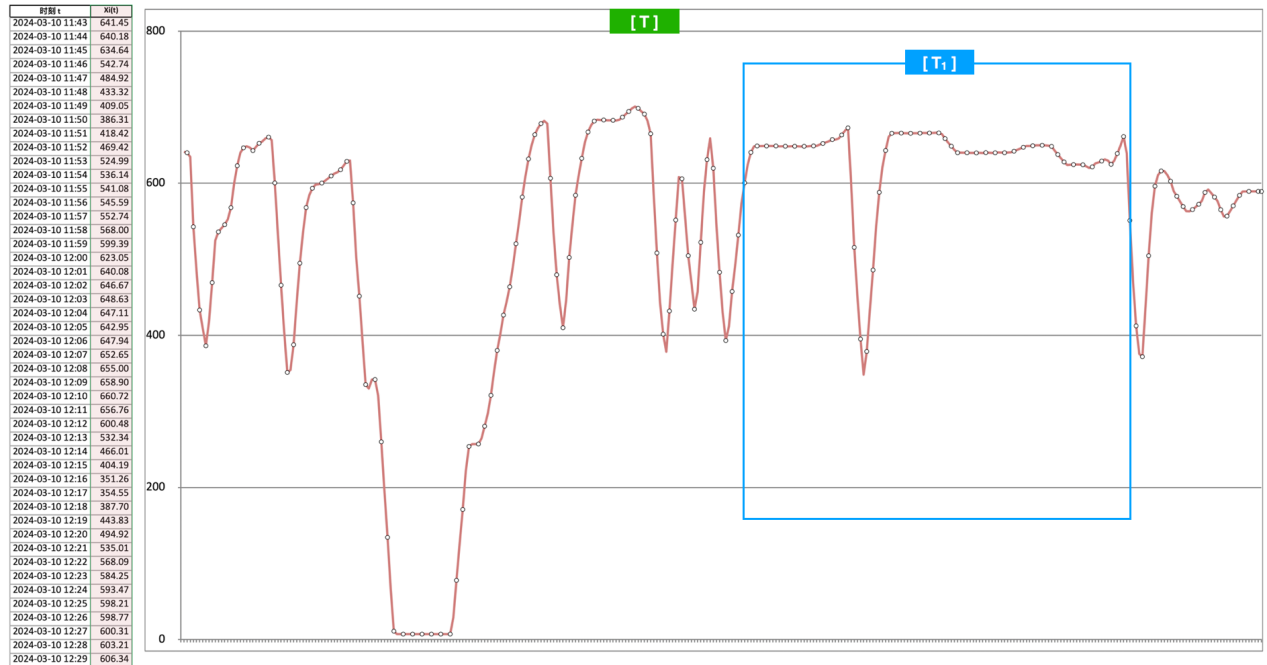
如果这些数据的曲线是这样的:
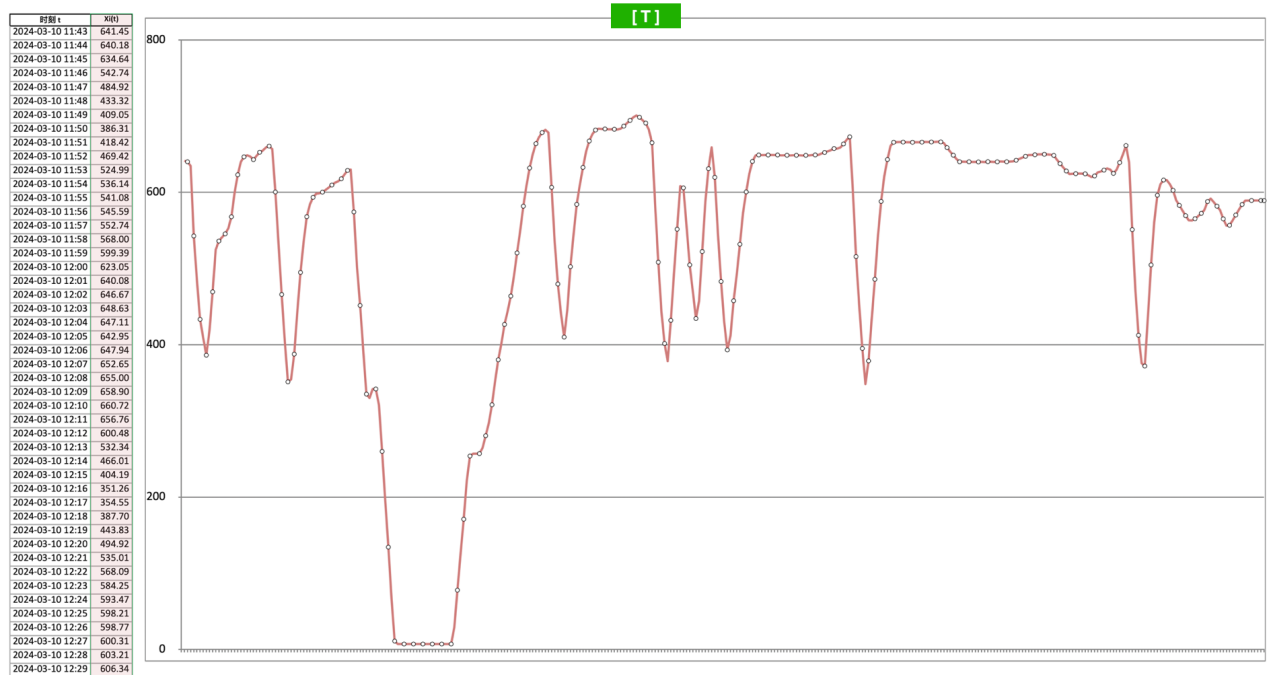
直观上就可以知道这个因素(变量)在这个[T]时段里可谓跌宕起伏,变化很大,给我们的感觉就是不稳定。
如果我们选择其中的[T1]时段的数据图表:
把 [T1] 时段的数据放大:
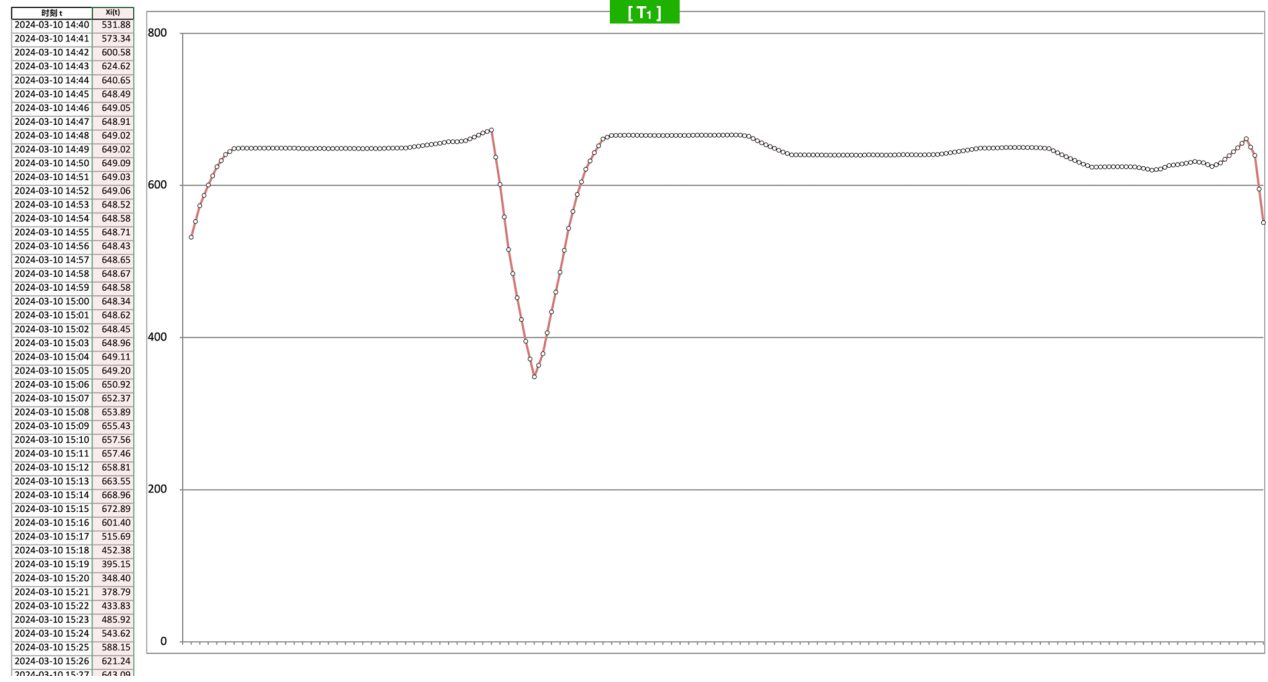
直观上应该也能得出结论,总体是稳定的,因为这个时段除了有三个比较大的变动,其他的变动都很小。
所以说到稳定性,就有两个相关的要素:第一个要素是时段,也就是说,我们所说的稳 定性如何,一定是某一个时段的稳定性;第二个要素是量化,也就是说,稳不稳定、有多么不稳定、有多么稳定,是需要定量的,需要有一个量化的方法。
关于单因素时序数据的稳定性,有很多专业的分析研究方法,如:
- ADF(Augmented Dickey-Fuller) 检验,是检测单位根的一种方法,用于判断时间序列是否是非平稳;
- KPSS(Kwiatkowski-Phillips-Schmidt-Shin)检验,是另一种测试时间序列稳定性的方法,它的假设检验与ADF相反,即检验序列是否具有单位根;
- PP(Phillips-Perron) 检验,方法与ADF检验类似,但在处理自相关和异方差的问题上有所不同,它适用于更广泛的情况;
- 变异系数(CV)检验,这是衡量相对变异性的一个统计量,通过计算标准差与均值的比值,可以用来评估时间序列的波动程度;
- 自相关函数(ACF)、偏自相关函数(PACF),可以帮助判断数据的稳定性和选择合适的ARIMA模型参数;
- Hurst 指数,是衡量时间序列长期记忆性的指标。指数值介于0和1之间,值越接近1,表示序列具有较强的趋势恢复能力,即长期依赖性。
对多因素(变量)的时序数据而言,稳定性的本质就是在某个时段里面,这些时序数据的总体离散程度的量化。这个离散程度,是指每个时序数据与该时段数据均值之间的离散程度。
