第4节 数据存储设置

数据存储设置，是管理员对本用户组织的数据保存期限的设置。

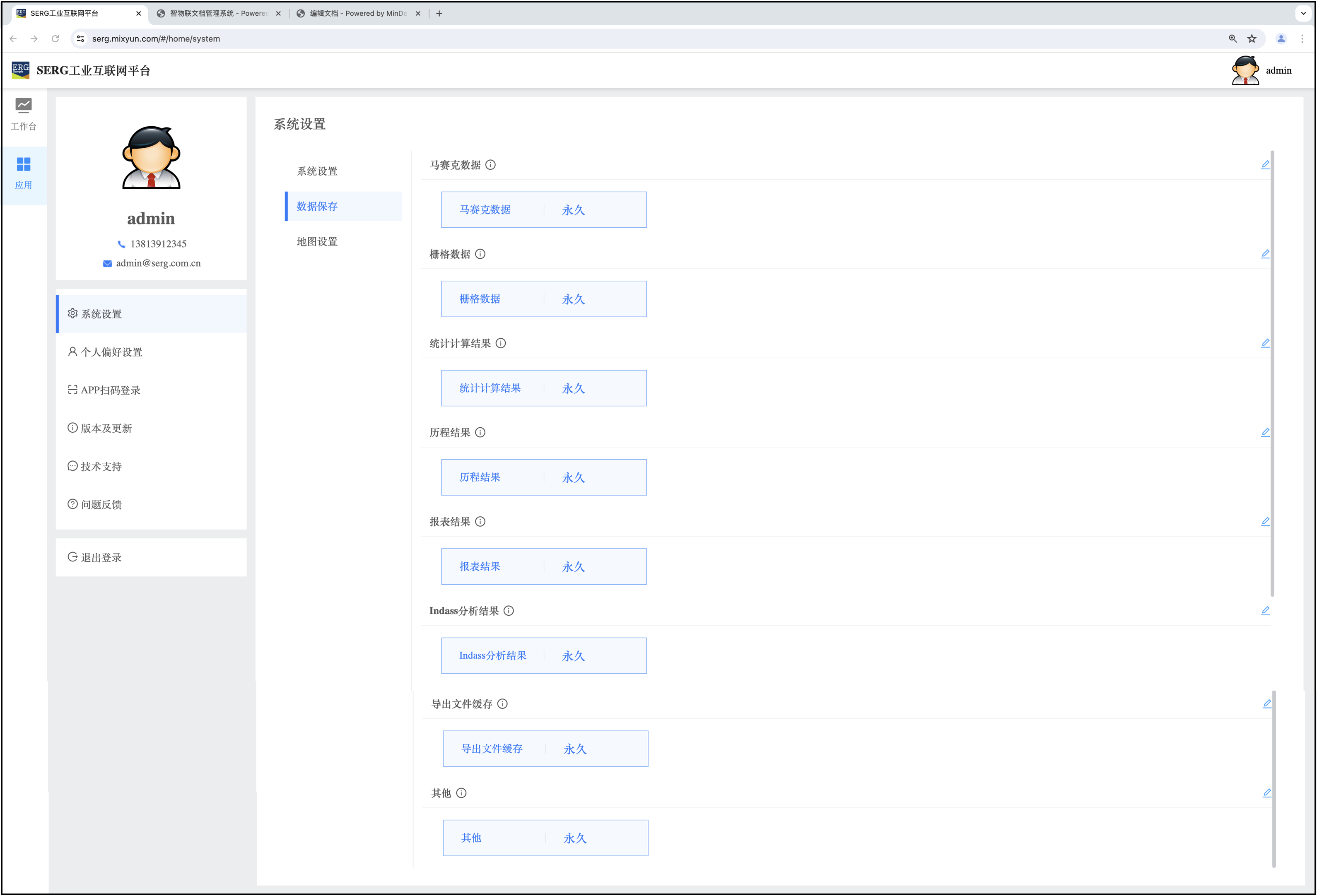
数据存储设定项

目前运行设置的数据存储项有：

• 马赛克数：对象的时序数据；
• 栅格数据：数据终端原始报文数据；
• 统计计算数据；“统计计算” 应用中，统计项目和计算项目所产生的统计结果和计算结果；
• 历程数据： “历程管理” 应用所产生的历程记录数据；
• 报表数据： “自动报表” 应用中，根据报表项目所自动产生报表的数据，包括表格；
• Indass分析结果数据：Indass（数据分析应用）的分析结果。包括，特征检测结果、特征统计结果、指数分析结果、偏态分析结果、稳定性分析结果、平衡分析结果、增量分析结果、以及风险分析结果；
• 导出文件数据：各种应用中导出文件的，如，对象实时数据导出的文件。

以上数据存储项都需要逐一进行设置，除此以外的 “其他”，则代表没有在上述列表中的应用的数据。

我们可以调整这些默认的数据存储设置：

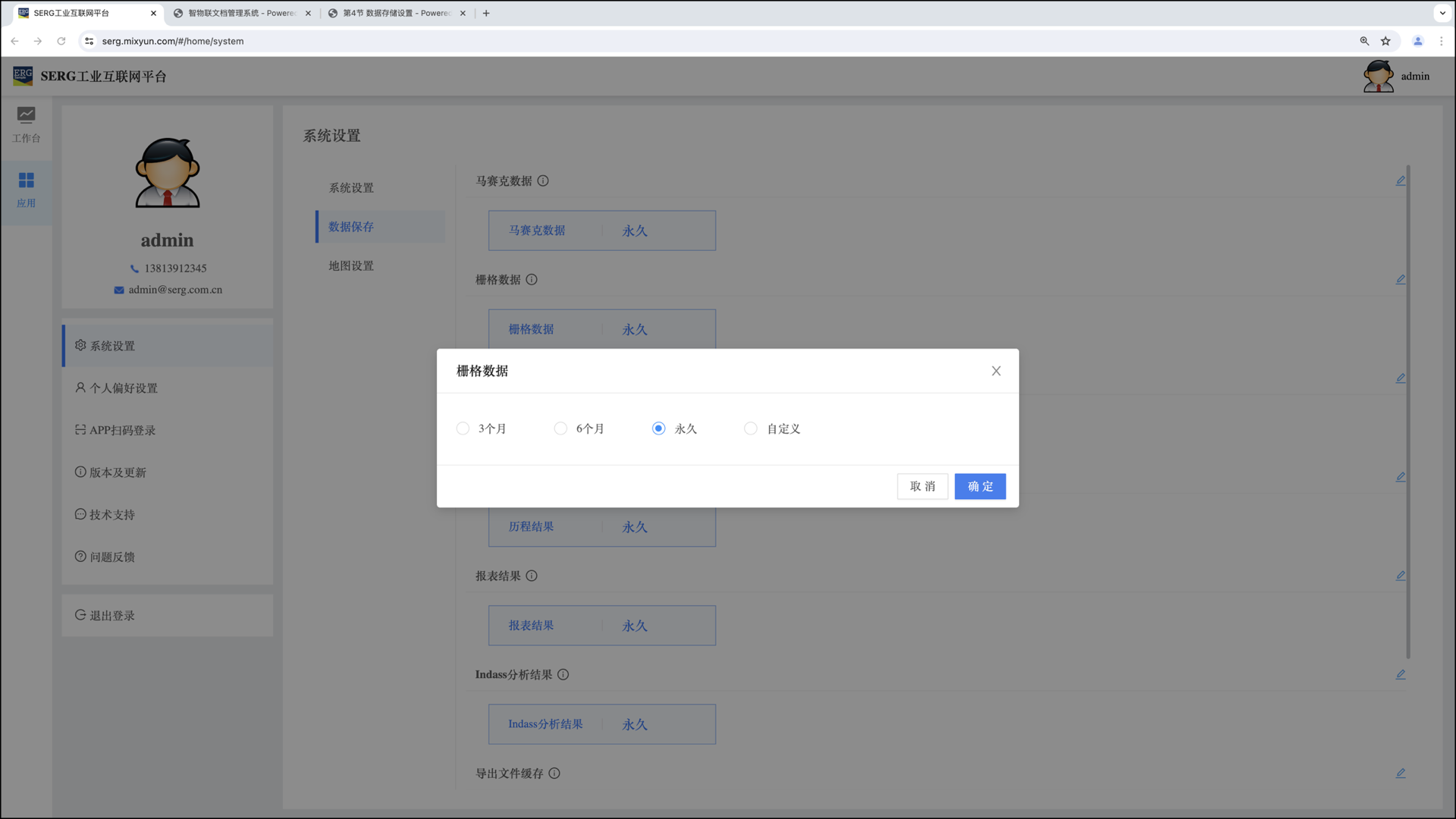
Mixiot SaaS 的使用其中一个收费项，就是数据存储量的占用收费。我们都知道，Mixiot 一旦使用，数据量就会不断增加，科学设置好数据的存储周期，可以避免不必要的资源浪费。

数据存储设置首先要考虑的当然是对数据保存的实际需求。同时，我们也要能大致估算出来，应用所产生的数据量会有多大，也就是每天会增加多少，这样也就能大致推算出每个月的数据量会有多少。

数据存储增量的估算方法

精确的数据存储增量的估算方法非常复杂，我们在这里介绍一种相对简单的估算方法。尽管这种估算方法有一定的误差，但这并不影响我们对数据增量的大致掌握，有助于我们更加科学合理的数据存储周期的设置。

栅格数据日增量的估算

第三方的数据终端（如，工业网关、DTU 之类的）我们目前取法提供有效的数据量估算方法。如果使用的是智物联公司数据终端（Aprus 适配器），我们可以按下面这个公式来大致估算每日所产生的报文数据：

$Q_d = \eta * K_n * C_m * (1 + \frac{\sqrt{K_n-K_m}}{2C_m})$

其中，

$Q_d$ 是每日数据增量，单位是 M（兆字节），这个就是我们需要的计算结果。

$\eta$ 是栅格存储估算系数，一般是 $\eta=0.2755$
$K_n$ 是适配器的总键值个数，也就是该适配器一共采集多少个参数
$K_m$ 是周期性报文的键值个数
$C_m$ 是所有周期性报文键值的报文周期的平均值，单位要换算成 “次/每分钟”

我们可以举个例子来解释。假设，我们要对某个适配器的报文进行估算，该适配器有30个键值，其中，5个键值是更新报文，25个键值是周期报文。这个 25个键值中，有5个报文周期是 10秒（6次/分钟）、有5个报文周期是 30秒（2次/分钟）、有5个是15秒（4次/分钟）、有10个是5秒（12次/分钟）。

那么，这个适配器每天的新增栅格数据的量，按照这个公式我们可以算出来是。首先，算出周期性报文的平均周期

$C_m=\frac{5 * 6 + 5 * 2 + 5 * 4 + 10 * 12}{25}=7.2$

然后，就可以套用计算公式：

$Q_d = 0.2755 * 30 * 7.2 * (1+\frac{ \sqrt{30 - 25}}{2 * 7.2})=68.75$

也就是说，这个适配器适配器每天的数据增量大约是 68.75（M）。

有了这个结果，我们也可以估算在这样一个报文周期设置下，这个适配器每天所消耗的流量$F_d$大约是$Q_d$的 75%，也就是：

$F_d = 0.75 * Q_d$

在这里，该适配器每天需要用的流量大概是 51.5（M）。

马赛克数据日增量的估算

马赛克数据（也就是对象时序数据）每天所产生数据增量的估算方法相对麻烦一些。

如果马赛克数据没有使用增量复制的压缩方法，那马赛克数据日增量的计算公式是这样的：

$M_d=\beta * N_v * \frac{1}{R_{mean}} * (1 + \frac{R_{mean}}{R_{max}+R_{min}} )$

其中，

$M_d$ 就是马赛克数据的日增量，单位是 M（兆）
$\beta$ 是马赛克估算系数，一般情况下，$\beta=2.83$
$N_v$ 是对象总变量个数，也就是对象的 FV 个数
$R_{mean}$ 是马赛克平均生成率
$R_{max}$ 是马赛克最大生成率
$R_{min}$ 是马赛克最小生成率

这里，$R_{mean}$是该对象所关联的全部适配器的$C_m$平均数的倒数；$R_{max}$是该对象所关联的全部适配器的 $C_m$的最小值的；$R_{min}$是该对象所关联的全部适配器的 $C_m$的最大值的倒数。

我们用一个例子来说明。

假设，某对象有 10个对象变量（FV），该对象关联的适配器有2个（1#适配器 和 2#适配器）。1#适配器的 $C_m=4$，2#适配器的$C_m=6$。

那么，

$R_{mean}=\frac{1}{5}=0.20$
$R_{max}=\frac{1}{4}=0.25$
$R_{min}=\frac{1}{6}=0.17$

这样就可以算出，该对象的马赛克日增量为：

$M_d=2.83 * 10 * \frac{1}{0.200} * ( 1 + \frac{0.20}{0.25 + 0.17})=208$

也就是说，如果没有使用增量复制的存储方式，这个对象每天新增马赛克数据的量大约是 208（M）。

需要说明的是，栅格和马赛克日增量的估算方法是一个包含经验的统计方法，存在一定的误差，在一般使用情况下的误差率约为 5-10%。

统计数据日增量的估算

统计数据的日增量，取决于统计项目的设置和相关属性。

我们看一下统计项目的属性设置，关键是两个，一个是统计/计算频次（P），另一个是统计对象个数（N）：

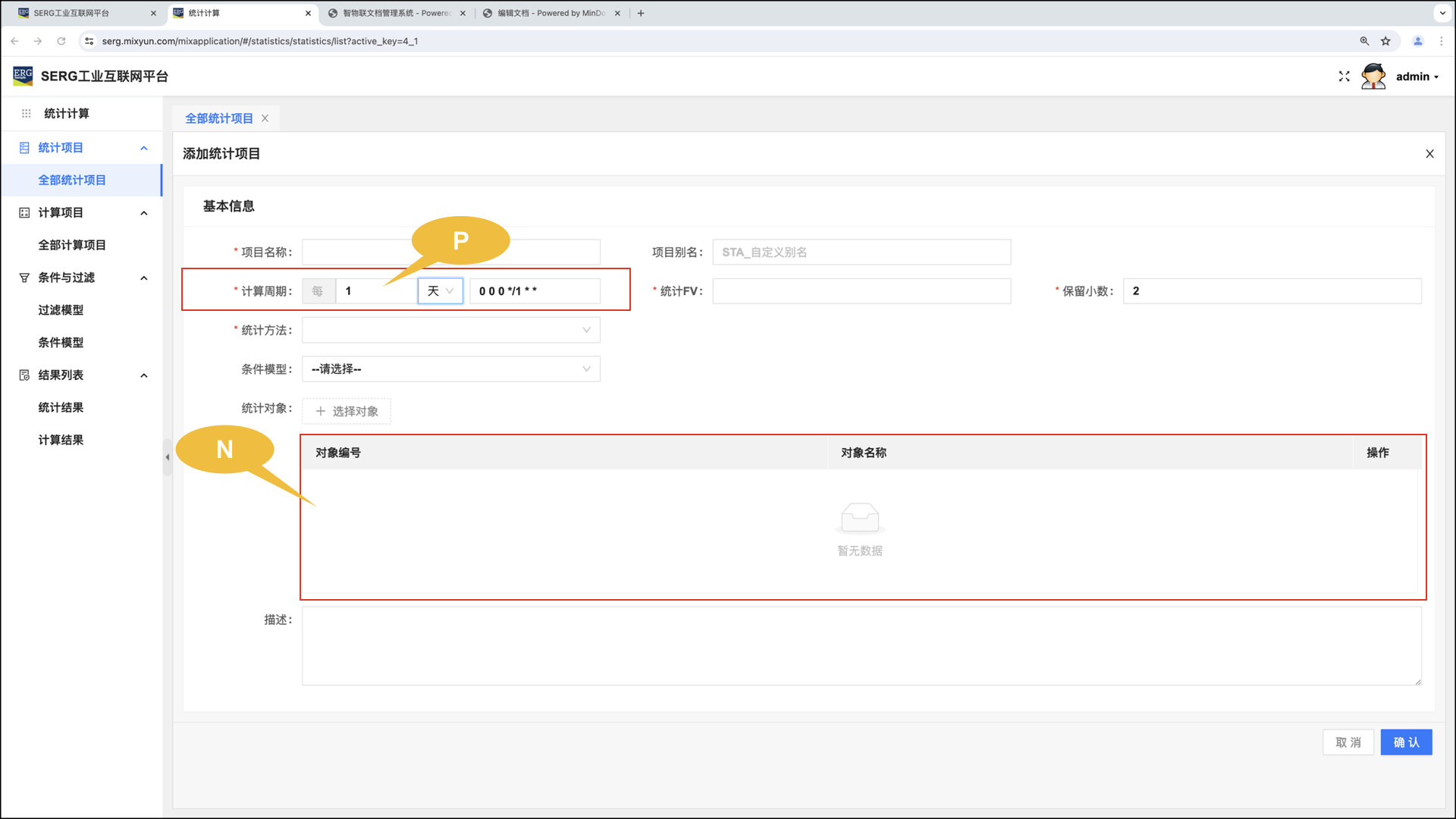
假设，一共有 $m$ 个统计项目，每个统计项目的统计频次为$P_i, (i=1,2,…,m)$ （需要换算成 次/每日），每个统计项目的统计对象个数为$N_i, (i=1,2,…,m)$，

统计项目 $i$ 的日增量$S_i$（单位 M）为：

$S_i=\lambda_s * (P_i+1) * N_i$

统计数据总日增量$S$为：

$S=\lambda_s*\sum_{i=1}^{m} (P_i+1) * N_i$

其中，

$\lambda_s$ 为统计数据量估算系数，一般情况下，$\lambda_s=0.00265$。

我们还是用一个例子来说明。

假设，我们一共有统计项目：

我们可以根据公式$S_i=\lambda_s * (P_i+1) * N_i$计算出每个项目的日增量：

由此可以计算出，统计项目计算结果的总日增量为 1.838（M）。

数据分析项目日增数据量估算

Indass 数据分析体系包括的应用有：指数分析、偏态分析、稳定性分析、平衡分析、增量分析，和 风险分析。这几个数据分析应用分析结果日增量的估算方法，与统计结果日增量的估算方法类似。

假设，分析项目的计算频次（P），分析对象个数（N）：

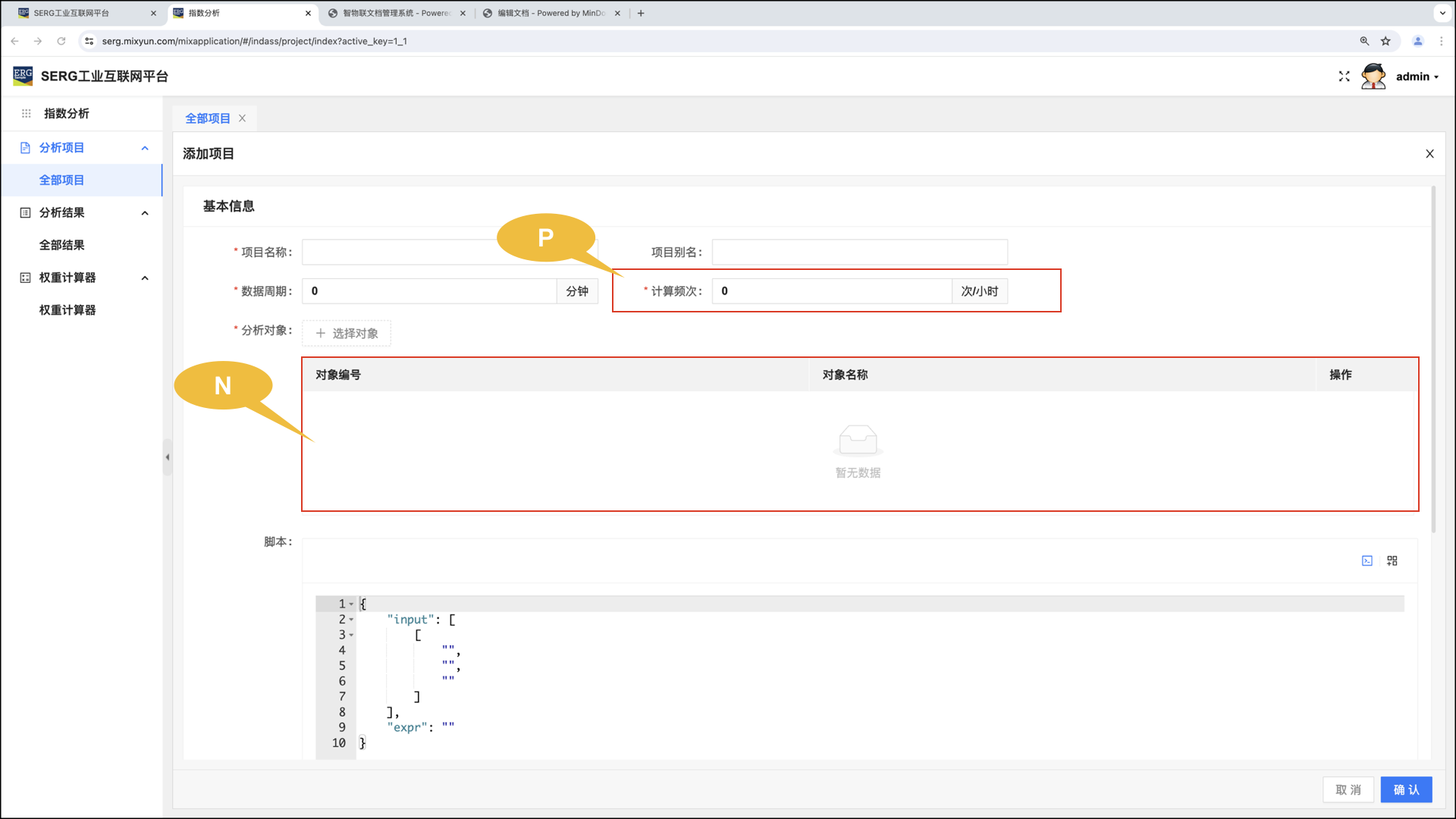
假设，我们一共有 $m$ 个分析项目，每个分析项目的计算频次为$P_i, (i=1,2,…,m)$ （需要换算成 次/每小时），每个分析项目的分析对象个数为$N_i, (i=1,2,…,m)$，

那么，分析项目 $i$ 的日增量$S_i$（单位 M）为：

$Q_i=\lambda_a * (P_i+1) * N_i$

分析数据总日增量$Q$为：

$S=\lambda_a*\sum_{i=1}^{m} (P_i+1) * N_i$

其中，

$\lambda_a$ 为统计数据量估算系数，一般情况下，$\lambda_s=0.00216$。

其他的数据量估算

除了上述应用项目的数据日增量估算方法以外，我们暂时无法提供其他应用的数据日增量估算，这是因为这些应用项目都是实时检测，如，特征检测，历程，等等。这些应用项目的结果不确定性非常大，很难有一个合理的估算方法。