MixIOT 体系中,很多地方(脚本)都要用到表达式。 MixIOT表达式跟编程算法语言的表达式基本类似,由操作符、操作数组成。
MixIOT 表达式操作符
- 算术运算,如:
+、-、*、/、%; - 比较运算,如:
==、!=、<、>、<=、>=; - 逻辑运算,如:
&&、||、!; - 其他运算,如:位操作
&、|、^、<<、>>、&^等。
操作数可以是数字、对象变量(FV)、函数调用结果等,运算符会对操作数进行处理。
如果表达式中包括有多个操作符和操作数,那么,表达式中的计算顺序由操作符的优先级决定。
MixIOT 表达式的操作符有不同的优先级,例如,乘除法操作符(*、/)会比加法操作符(+、-)有更高的优先级。在没有括号的情况下,会先计算乘除法,再计算加减法。
结合性是操作符相同优先级时的计算顺序,默认都是左结合性,比如,1-2-3等价于(1-2)-3。
MixIOT 表达式会根据操作符的优先级和结合性规则,从左到右逐步求值。
MixIOT 表达式中可以包括函数调用,它由函数名和跟随的括号组成,括号内可以包含零个或多个表达式作为参数,例如math.Sqrt(x)。
内建函数
MixIOT 表达式支持的内建函数如下。
算术函数
- Abs(x):计算并返回 x 的绝对值
- Cbrt(x):计算并返回 x 的立方根
- Ceil(x):计算并返回大于或等于 x 的最小整数
- Copysign(x, y):返回一个值,其大小与 x 相同,符号与 y 相同
- Exp(x):计算 e 的 x 次方
- Expm1(x):计算 e 的 x 次方减 1
- Floor(x):计算并返回小于或等于 x 的最大整数
- Hypot(p, q):计算直角三角形的斜边长度(即 p 和 q 的欧几里得距离)
- Log(x):计算并返回 x 的自然对数
- Log10(x):计算并返回 x 的以 10 为底的对数
- Log1p(x):计算并返回 1+x 的自然对数
- Mod(x, y):计算 x%y 的浮点数余数
- Pow(x, y):计算 x 的 y 次方
- Round(x):四舍五入 x 到最近的整数
- Sqrt(x):计算并返回 x 的平方根
- Trunc(x):计算并返回 x 的整数部分
三角函数
- Acos(x):计算并返回 x 的反余弦值
- Asin(x):计算并返回 x 的反正弦值
- Atan(x):计算并返回 x的反正切值
- Atan2(y, x):计算并返回点 (y, x) 与 x 轴正方向之间的角度
- Cos(x):计算并返回 x 的余弦值
- Sin(x):计算并返回 x 的正弦值
- Tan(x):计算并返回 x 的正切值
超越函数
- Acosh(x):计算并返回 x 的反双曲余弦值
- Asinh(x):计算并返回 x 的反双曲正弦值
- Atanh(x):计算并返回 x 的反双曲正切值
- Cosh(x):计算并返回 x 的双曲余弦值
- Sinh(x):计算并返回 x 的双曲正弦值
- Tanh(x):计算并返回 x 的双曲正切值
特殊函数
- Erf(x):计算 x 的误差函数
- Erfc(x):计算 x 的互补误差函数
- Gamma(x):计算 x 的 Gamma 函数
- Lgamma(x):返回 Gamma(x) 的自然对数和符号
误差函数( Error Function,记为 ) 是一个特殊的非元素函数,定义为:
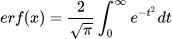
其中,
是高斯积分的一部分, 而误差函数在概率论中尤其有用,因为它描述了正态分布的累积分布函数。
互补误差函数(Complementary Error Function,记为 )是误差函数的补充,定义如下:
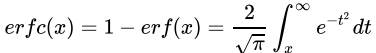
互补误差函数用于计算高斯分布中超过一个给定界限的尾部概率。在统计学中,当从正态总体中进行抽样时,它告诉我们随机变量落在距均值多个标准差之外的概率。
Gamma函数(通常表示为 Γ(z) )的定义是通过一个无穷积分给出的:
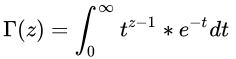
这个积分称为 Euler(欧拉)积分的第二类,具有这些性质:
- 递推关系:
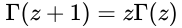 。
。 - Γ(1)=1,因为
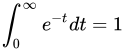 。
。 - 对于非负整数n,
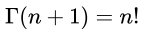 。
。 - Γ 函数在 z = 0,-1,-2, … ,有简单极点。
文档更新时间: 2024-07-12 21:07 作者:Mixiot
