第2节 “风险分析”的使用方法

（一）进入风险分析应用

跟其他Indass应用—样，“风险分析”有两个板块，—个是分析项目，—个是分析结果。

我们从创建项目开讲解风险分析的使用方法。创建项目后，把脚本切换到界面化：

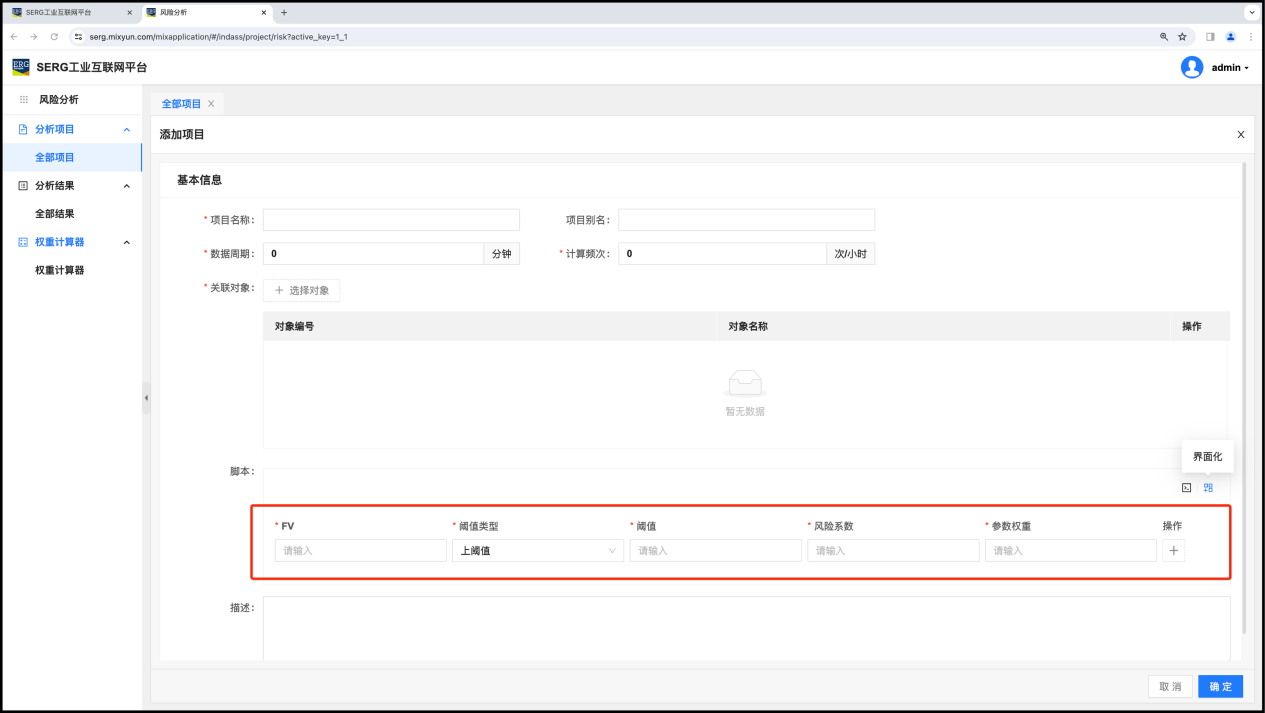
从这个创建交互可以看到， 一个风险分析项目，除了名称（别名）这些基本属性，以及计算数据周期和计算频次配置，选择风险对象以外，剩下的就是选择风险因素。

再看看风险因素，这里有几个重点：

1. 风险因素的选择，就是FV变量的选择；
2. 风险因素的阈值；
3. 风险因素的权重；
4. 风险因素的风险系数。

来解读一下它们的含义。

首先，我们需要选择合理的风险因素，当然，这些都是风险研究对象的变量，这些因素（变量）必须是风险相关的因素，而且是有阈值限制的。

如果一个风险分析项目包括多个风险因素，那么还需要给这些风险因素配置相关的权重。

除了风险因素的权重，还需要给这些风险因素配以对应的 “风险系数”。“风险系数” 是某风险因素引发风险发生的可能性或导致风险的程度。风险系数是一个无量纲标量，而且大小没有限制，在创建风险分析项目的时候，可以独立定义这个风险系数的大小。

风险因素的“风险系数”不同于“权重”。权重是在这个分析项目组所选择的风险因素对在这个风险分析项目中的重要性，这个重要性是通过风险因素之间的两两比对（决策）矩阵计算出来的，权重的关键概念是重要性。而风险系数则是该风险因素可能引发风险发生的可能性，以及一旦这个风险发生受该因素影响的程度。

（二）创建风险分析项目

现在正式来创建一个风险分析项目。

（1）选择风险研究对象

首先，需要确定分析什么风险，选择什么作为风险研究对象。

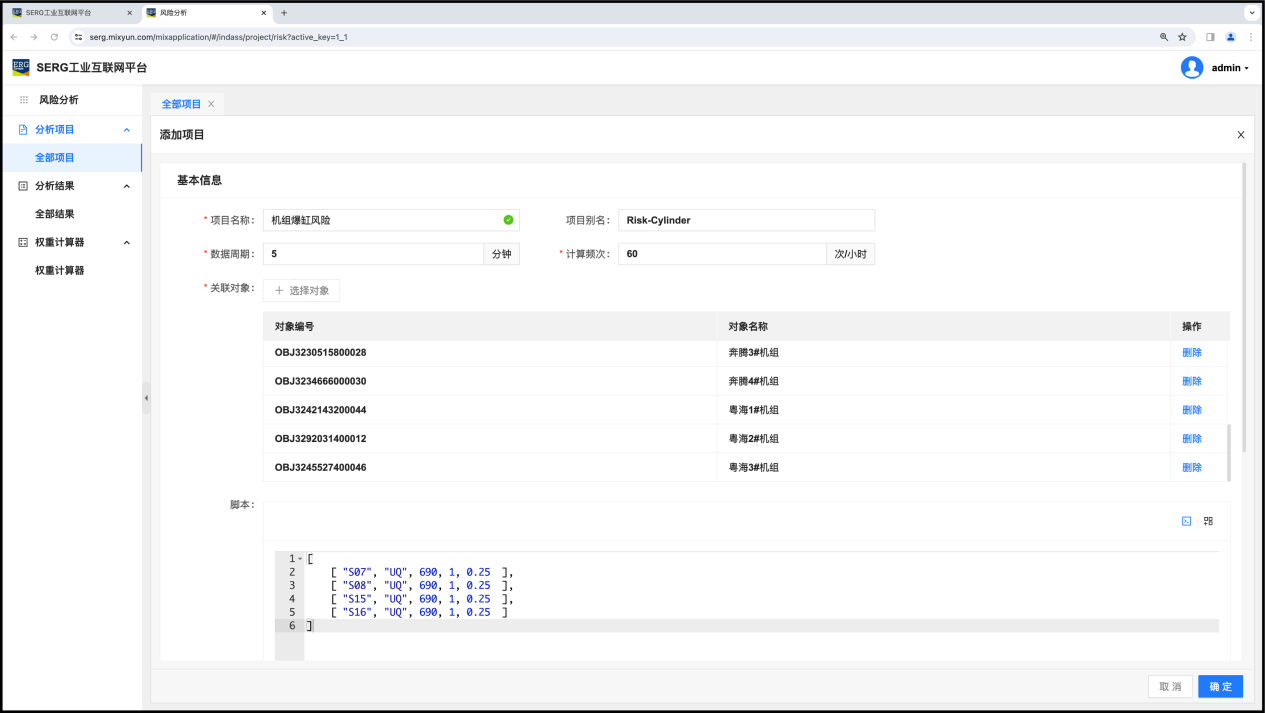
在瓦斯发电这个项目中，我们选择发电机组为风险研究对象，分析的是“机组爆缸”的风险。所谓机组爆缸，也就是机组的缸温过高，最终导致机组的气缸损毁。

（2）选择风险因素

根据这个风险分析的命题，我们选择机组A/B侧缸温作为风险因素。

这里需要说明的是，“风险分析”规定的风险因素最多只能是4个。这是因为风险分析的计算非常复杂，计算量非常大，需要消耗大量计算资源。最多4个风险因素的规定，基本上是可以满足绝大多数风险分析需要的。

所以，我们选择 A1/A2 以及 B1/B2 这4个气缸缸温作为风险因素。

（3）确定风险因素边界

气缸风险阈值的限定范围是不能超过690°C，也就是因素的“上阈值（UQ）”等于 690。

（4）确定风险因素权重

因为风险因素相同，所以它们的权重是一样的，各四分之一，都是0.25；

（5）确定风险系数

风险因素的 “风险系数” 和 风险因素的 “权重” 是两个不同的概念，权重是针对全部因素这个整体而言的，是风险因素之间的相对重要性；

而风险系数是针对单个因素而言的，是指这个因素导致风险结果出现的可能性大小的一个度量。我们可以这样来理解：假设只有这个因素的话，由于这个因素导致发生某种风险事故的可能性（概率）有多大。

风险因素的范围用简单的方式来标定，理论上是 0~1 之间的任何实数。但我们建议取值为 0.1、0.2、0,3，….，0.9、1.0 这样的一位小数。

如果我们不能确定某个因素的风险系数，可以不填写。也就是说，风险系数项是可选项，其规则是，要么都不填，要么都要填。如果都不填，则在风险估计值计算的时候，风险系数默认为都是 0.5。

这里需要说明的是，虽然我们使用权重计算器去量化权重，但量化权重的过程是给定两两因素的比度值，这个环节实际上也是一个主观的判断。而风险系数的确定，最好是能根据一些历史的数据或统计结果。

（三）分析脚本

风险分析脚本的规范是：

[
    [ "风险因素FV", "UQ",  上阈值,  风险系数,  权重 ],
    [ "风险因素FV", "LQ",  下阈值,  风险系数,  权重 ]
]

在这个风险分析项目中，脚本就是：

[
    [ "S07", "UQ", 690, 1, 0.25 ],
    [ "S08", "UQ", 690, 1, 0.25 ],
    [ "S15", "UQ", 690, 1, 0.25 ],
    [ "S16", "UQ", 690, 1, 0.25 ]
]

有了这些，就可以创建风险分析项目了

（四）风险分析结果

保存风险分析项目后，可以在操作菜单启动该项目的运行：

跟其他的Indass应用一样，风险分析计算结果是风险估计值。

风险估计值的计算方法有两个方面的考量，一个是出现风险的实时可能，另一个是出现风险的累积可能。

风险估计值曲线（风险曲线）的解读并不难，根据风险值的计算方法，需要掌握这么几个解读分析结果的重点：

1. 掌握风险曲线的稳定水平。也就是说，在一段时间里面，风险估计值是不是都在某一个范围内小幅变化。这个范围也许会是变化的，但在一个连续时间段内，这个范围应该是恒定的。
2. 如果在一个相对长的时间段里面，找不到相对恒定的风险值范围，也就是说，在一段时间里面，风险估计值是跌宕起伏，波动不停，没有规律，那就需要重新去对风险项目进行检查，一方面是要看一下所选择的风险因素是不是恰当，另一方面是检查各风险因素的权重和风险因素的风险系数。
3. 掌握风险曲线的变化。也就是说，比起风险估计值的水平（值的大小），风险值的变化更加重要。如果风险估计值在一个时间段持续增加，而且有继续增加的趋势，则引发风险的可能性增加。

假如计算出来的风险估计值曲线是这样的：

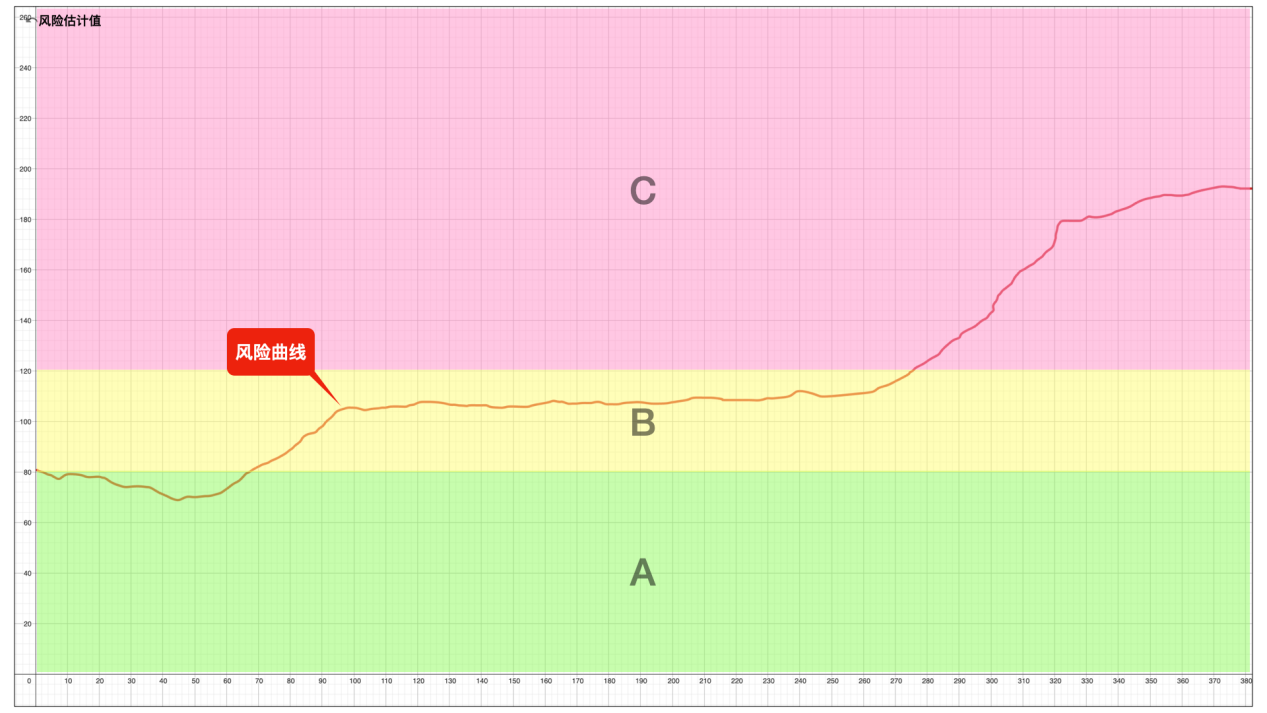
这样子的风险曲线，也就是风险估计值结果，应该是比较标准的。
我们在分析这个风险结果时，可以这样做：

1. 找到B区域，这个区域可能会反复出现，找到B区域非常重要。找到B区域后，要反过来观察所设置的风险因素的变化情况，并找到以往的数据记录，查看这个区域里面有没有出现过风险的相关记录。换句话说，我们根据实际情况来确定这个B区域，而且要保证风险曲线在这个区域内，是没有出现过所对应的风险事件或风险状态。
2. 在B区域之下，可以作为一个安全区域A来定义。
3. 在B区域之上的C区域，可以作为一个重点的风险范围来考察，但这是一个需要花一些时间，而且需要后续对各种数据进行再次分析的工作。理论上来说，风险估计值与风险事件（或风险状态）的发生是有一个正相关关系的，但风险估计值并不等同于风险事件发生的概率。

如果风险分析结果是这样：

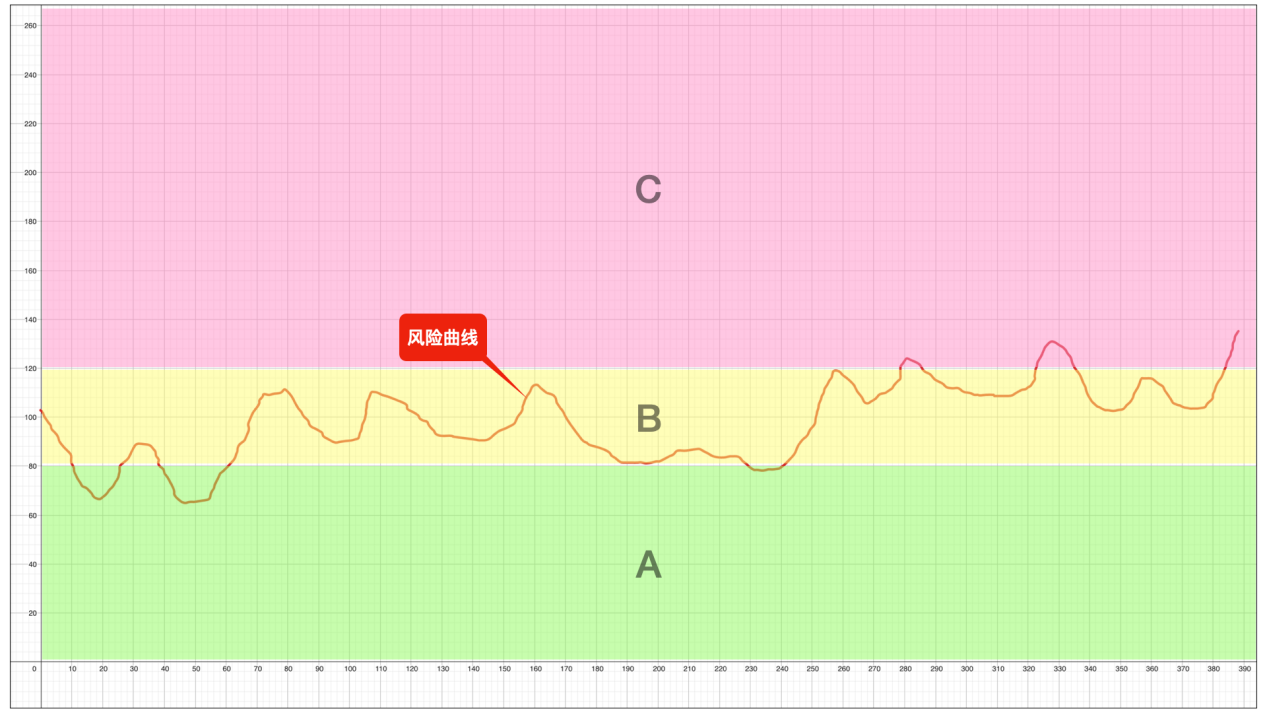
这种情况也是最可能遇到的情况。与前面一种情况类似，首先还是要找到B区域，如果能找到B区间，就可以确定A区间和C区间。
重点是，我们要在C区间的数据，找到风险估计值与风险发生概率的关联关系。

（五）风险概率

前面解释过，风险分析项目的计算结果是风险估计值。风险估计值与风险分析项目所对应的风险事件发生或风险状态发生的概率（我们称为风险概率），在理论上是存在正相关关系的，但风险估计值本身并不是风险概率。

事实上，风险估计值与风险发生的概率之间的对应关系是比较复杂的，我们还需要使用其他的分析方法来实现这个对应的大致关联。但对各种不同工业场景，不同的工况条件，这些分析方法都有一些差别。

我们可以对分析方法做一些基本的介绍，这是为了在未来能把这些分析结果用起来，让它们发挥作用 。

（1）风险模型

风险估计值输出的结果，作为数据，是可以用来作为风险模型分析的。风险估计值适合的风险模型是 “折叠风险模型（Folded Model） ”。

折叠风险模型听起来可能有点复杂，我们可以用一个更直观的方式来理解它:

想象一下，有一张纸，上面画着一条线，这条线代表了收集的数据点。如果这张纸上的线形状非常不规则，有很多尖峰和低谷，就像是在数据中存在很多偏斜或异常值。如果我们试图直接在这个不规则的线上分析数据或预测未来的点，会很困难，因为这些尖峰和低谷会干扰我们的分析。

这时，折叠风险模型就像是用手轻轻地折叠这张纸，使线变得更平滑一些。在现实中，这个“折叠”的过程不是物理上的，而是通过数学变换来实现的。我们可能会调整数据中的某些值，或者以某种方式重新解释它们，目的是减少极端值的影响，使整体数据分布看起来更加接近正常情况，从而更容易进行分析和预测。

然后，在这个更平滑、更规则的基础上来构建模型，这就像是在较平整的纸上画线。因为数据现在更加“正常”和规则，所以我们的模型可以更准确地理解数据的真实结构，进而做出更好的预测。最后，当得到模型的预测结果时，我们可能需要做一些调整，把这些结果“转换回”原来的尺度，以确保它们对于原始的数据是有意义的。

所以，简而言之，折叠风险模型就是一种让数据更易于分析和预测的方法，通过减少数据中的极端值和偏斜，使我们能够构建更准确的模型。

（2）建立折叠风险模型的方法

假设，我们有某个时段的风险估计值计算结果数据集 R:

$R= ( r_1,r_2,…,r_n )$

我们需要找到一个折叠变换函数，g(·)， 目的是通过“折叠”减少数据的偏斜，使其分布更加接近正态分布。折叠变换的选择依赖于数据的性质和分布特点。例如，对于界限在 [0, 1]区间内的数据，可以考虑使用

$g(r)= min(r,1-r)$

这样，原有的风险估计值数据集结果经过折叠变换后的数据集就变成了g(R)：

$g(R)=(g(r_1),g(r_2),….,g(r_n))$

也就是说，我们需要用 g(R) 数据集构建风险概率模型。假设使用线性回归模型，模型可以表示为：

$g(r_i)=\beta_0+\beta_1X_1+\beta_2X_2+….+\beta_kX_k+\epsilon_i$

$i=1,2,3,…,n$

其中，

$X_1,X_2,X_3,….,X_k$ 是解释变量，
$\beta_1,\beta_2,\beta_3,….,\beta_n$ 是模型参数，

而

$\epsilon_i$ 是误差项。

对于预测或分析目的，得到模型估计结果后，可能需要将这些结果反转换回原始的数据尺度，也就是要把之前的折叠变换 $g(.)$ 进行逆变换。

折叠模型的使用也不是一件容易的事情：

• 折叠变换的选择对模型的性能和解释有重要影响，不同的数据可能需要不同的折叠方法；
• 折叠变换后，模型的解释复杂度可能增加，因为关系是在变换后的尺度上定义的；
• 数据的某些特征或极值可能在折叠变换后不再明显，这可能对模型的准确性和解释性产生影响。

通过这个框架，折叠风险模型提供了一种处理偏斜数据、提升模型准确性和适用性的方法，但它的成功实施高度依赖于对数据特征和所选变换方法的理解，而现在我们可以尝试使用AI，也就是神经网络和机器深度学习的方法。

（六）随机微分方程

把风险估计值 “换算” 成风险概率，这是一件非常复杂的事情。虽然有上面介绍的折叠模型方法，但真正用起来也不是一件容易的事情。我们可以理解为，这是一种 “精确” 的做法。

事实上，风险估计值本身也是有巨大价值的。如果风险估计值不断增加，发生风险事件的可能性就会增加，如果能掌握风险估计值的趋势，适时做出预警，也是一件有价值的事情。

我们可以这样来理解风险估计值：

风险估计值的增加，就好像我们在折弯一根竹子。竹子有一定的韧性，并不会一开始就折断。

但最终在某个时刻，当弯曲达到某个程度的时候，这根竹子会在某一个位置上被折断。

这个竹子的弯曲程度，就是风险估计值的大小；而竹子的折断，就是风险事件的发生，或者风险状态的出现。

虽然我们知道，这根竹子弯曲下去早晚都会折断，但很难确定两个事情，一个是竹子折断的时刻，另一个是折断在什么位置。

这两个很难确定的事情，实际上都取决于我们怎么去了解这根竹子的韧性如何，也就是说，我们要对风险估计值有一个深刻的理解。

这可以借助伊藤随机微分方程（ITOH Stochastic Differential Equations）的方法，这个微分方程的一般形式是：

$dR_t=C(t,R_t)dt+B(t,R_t)dW_t$

其中， $R_t$ 就是风险估计值，可以认为这是一个随机过程，随时间变化的随机变量；

$B(t,R_t)$ 是随机波动项的系数，描述了 $R_t$ 的随机波动，就是 $B$ 区域的波动性；

$C(t,R_t)$ 是确定性漂移项，描述了 $R_t$ 的确定性变化趋势，就像是在 $C$ 区域的变化趋势；

$W_t$ 是布朗运动，可以理解为一个随机项。

总结一下，上面说的这些内容，只是说明这个风险估计值的深度利用，能与实际工业生产过程中的风险相对应，可以在解决安全生产的实际问题。